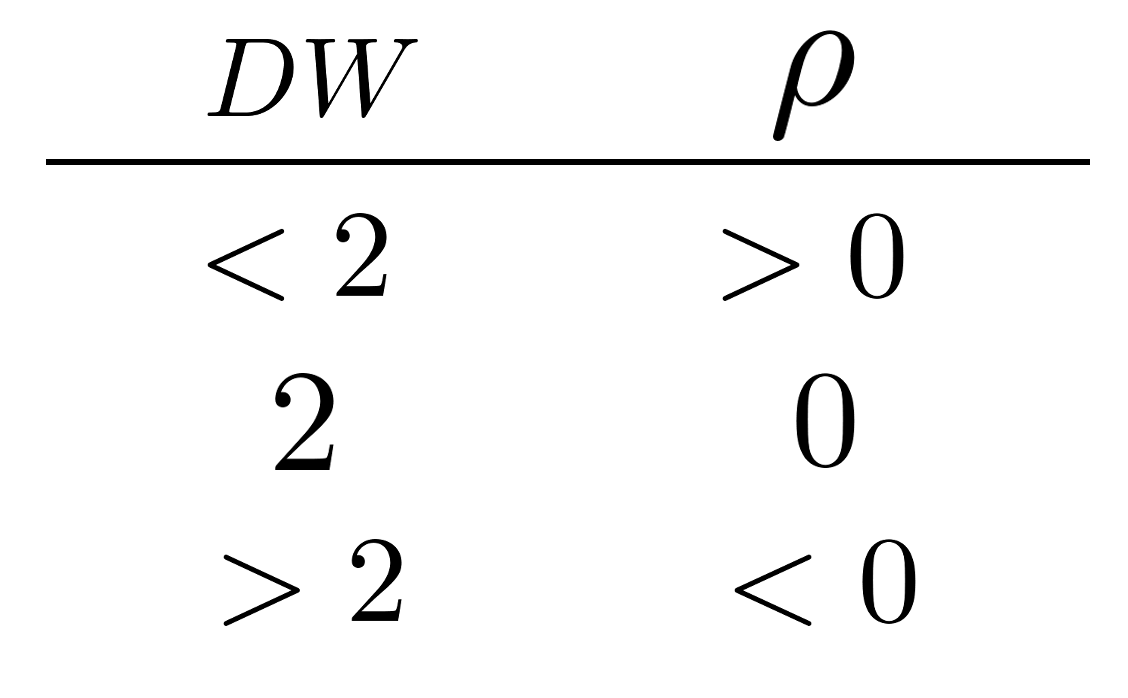Syleir’s note

2020.4.1より統計検定やE資格の勉強の進捗を報告しています。統計検定準1級、E資格、G検定取得しました！当ブログへのリンクはご自由にどうぞ。

MENU

【統計検定準1級】ベイズ統計学を勉強するための教科書について触れる

統計検定

統計検定準1級、最近機械学習に対する出題が増加傾向にあります。以前は無視してもよい分野だったのですが、そうも言ってられなくなってきました。統計検定のバイブルと言っても過言ではない日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック、とても良い本なのですが、ベイズ周りの記述がかなり浅く、概念の理解に繋がりにくいのが難点です。

そこで本日はレベル、目的別にベイズ統計学の理解につながる教科書、本をいくつか紹介したいと思います。

 

1. まずはここから！ベイズ統計学の初歩

史上最強図解　これならわかる！ベイズ統計学

史上最強図解　これならわかる！ベイズ統計学

Amazon

この本はベイズ統計学ってなに？ベイズの定理を高校で習ったことはあるけど...くらいの方が対象です。自分もこの本から入りました。この本は少し古い（2012年）のですが、古典的な頻度論とベイズの考え方の違いを同じ例を使って説明してくれたり、図や表、説明、具体例を交えながら解説してくれるのでとてもおすすめです。非常に簡単な例から始まって最終的にはナイーブベイズフィルターやMAP推定、ベイジアンネットワークまで応用を触れてくれる本です。初歩のうちから応用、実用を見据えて勉強するのは非常に役に立つので良いかと思います。

syleir.hatenablog.com

一応2年前の自分の黒歴史クラスの記事ですがレビューもあります。

2. ベイズ統計の名著で考え方を学ぶ！

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

Amazon

この久保先生の本は名著です。自分の周りにいる統計検定合格者のみならず、ベイズを勉強している人はこの本で学んでいる人が非常に多いです。この本の良いところは、前提知識が高校数学程度で書かれている割に、到達点がかなり高いところです。数式のいじり方を書いてくれている本はありますが、この本は統計モデリングの方法を書いてくれています。実際の解析でのピットフォールや、モデルの限界、その先の対処法を書いてくれているので非常に勉強になります。最初は非ベイズでのモデリングから始まりますが、最後の方の章ではMCMCや階層ベイズなどベイズモデリングによる解析まで触れてくれます。統計パートは実装は大部分がRですが、Rがわからなくても理解ができるような構成になっています。

3. 待望の和訳版出版！数式的な解析を学ぶ

標準 ベイズ統計学

標準 ベイズ統計学

  • 朝倉書店
Amazon

この本は2009年にワシントン大学の院の講義ノートをもとに英語版が出版され、ベイズ的な統計モデリングの初歩を学ぶ本として有名でしたが、時は2022年、ついに和訳され日本語での入手が可能になりました。最初の方の章ではベイズ統計の考え方について触れ、徐々に共役事前分布の計算方法と導入が進み、階層ベイズモデリングやMCMC、混合モデルへと進んでいきます。統計ソフトを利用した実装も紹介されていますが、Rを用いた実装になっています。

やや和訳がわかりにくいところや説明が難しいところがありますが、非常に勉強になります。ただ統計検定準1級レベルとしてはややレベルを超越しているところがあるので余力、あるいは興味がある人向けになるでしょうか。

 

4. 1冊でMCMCの理解を深める！

ゼロからできるＭＣＭＣ　マルコフ連鎖モンテカルロ法の実践的入門 (ＫＳ理工学専門書)

ゼロからできるＭＣＭＣ　マルコフ連鎖モンテカルロ法の実践的入門 (ＫＳ理工学専門書)

Amazon

MCMCのアルゴリズムが一冊で本にまとめられています。この本の良いところは実装が著者のgithubで複数言語で書かれているところです。C++とPythonがあります。

GitHub - masanorihanada/MCMC-Sample-Codes: Code for simple Markov Chain Monte Carlo simulations, for beginners

普通の本だと1章分くらいしか書かれていないところを本1冊使って書かれているので説明が重厚でわかりやすいです。とてもおすすめです。

 

5. 実際に実装してみる

Ｐｙｔｈｏｎではじめるベイズ機械学習入門 (ＫＳ情報科学専門書)

Ｐｙｔｈｏｎではじめるベイズ機械学習入門 (ＫＳ情報科学専門書)

Amazon

 

Pythonで動かして学ぶ！あたらしいベイズ統計の教科書

Pythonで動かして学ぶ！あたらしいベイズ統計の教科書

Amazon

統計学はベイズに限らず、自分で実装するのが一番勉強になります。そんな時の本を紹介します。

僕はRとPythonを主に使いますがPythonが一番使い慣れているので、Pythonで実装を学ぶのが一番ストレスがなく勉強になります。同じような方はいると思うので実装を学びたい方のための本を紹介しておきます。特に上の本は2022年出版で新しいのでライブラリも比較的新しいものが使われててモダンな実装を学べてよいです。

6. さらなる学習のために

パターン認識と機械学習 上

パターン認識と機械学習 上

Amazon

本当に余力がありさらなる学習をしたい人にはパターン認識と機械学習（PRML）がおすすめですが、統計検定的にはオーバーワークです。この本は古典的名著で、情報系大学生や院生の輪読でよく使われているので、独学したい人はその辺の資料をネットで探してみると少しは読みやすいかもしれません。下巻もあります。余力があればぜひ。

 

以上、ベイズ統計を学ぶための本を紹介していきました。統計検定対策的な意味だと上から順番に勉強していくのが良いと思います。少しでも参考になれば。

【AtCoder】Boot Camp for Beginners を完走しました。【所要時間3年】

はじめに

最近はAtCoderという競技プログラミングサイトで遊んでいます。AtCoderは豊富に過去問があり、それらがまとまっているAtCoder Problemsというサイトにお世話になっています。AtCoder ProblemsのサービスとにはBoot Camp for Beginnersという、AtCoderの教育的な過去問を解くことができるサービスがあります。全300問で100問ごとにEasy、Normal、Hardと難易度が別れており、それぞれ灰、茶、緑diffが中心の問題となり、Hardの後半から水diffが混ざってきます。

今日はこれを完走したよ！というお話です。

Boot Camp for Beginners のレベル感

Easyの前半はプログラミングを始めたばかりでも解ける問題が多いですが、Hardの後半は1日1問解くのも結構しんどくて、ずっと解けない問題もありました。長く考えていると解法が湧いてきたりして初めて見てから3ヶ月経ってから正解したような問題もあります。

 

最初の方は文字列操作が多かった印象ですが、後半は幅優先探索や二分探索、かなり考察が必要な数学問も増えてきて解き応えがかなりありました。

 

完走までの期間、レーティング推移


 

実は完走までには3年弱経過しています。最初にこの問題セットに取り掛かったのは2019年9月で、現在は2022年6月になってしまいました。2019年の時は精進といえばBoot Camp for Beginnersだったような気がしているのですが、時が経つに連れてみなさんは競プロ典型 90 問などで勉強しているようで、時代の波に取り残されてしまったなあという浦島太郎感を味わっています。

最初のAC

現代、AtCoder参加者のレベルがインフレしているような指摘もありますが、現在でも通用するような良問が入ったセットで、だんだん難しくなっていく様も勉強していてかなり役立ち、自分の解けるギリギリの問題が出題され続けるのも非常によかったです。

精進を始めた頃はレートも353でしたが、現在は1070と順調に(?)上昇しており、かなりレーティング上昇に寄与していると実感しています。Boot Camp for Beginnersを始めてからパフォーマンスの下界が上がったような感じで、コンテストで大失敗することもなくなり、平均パフォーマンスもかなり上昇してきました。ABCのA-D問題で使うかなりの手法を学べるので、早く解く練習にもなり、漏れなく勉強できるのでおすすめです。

 

解くのに必要なアルゴリズム

解くのに必要なアルゴリズムはそんなに多くなく

・初歩的なDP
・尺取り法
・二分探索
・全探索、Bit全探索
・幅優先探索、深さ優先探索
・累積和

くらいです。PAST本でいうと第6章くらいまでの知識で十分です。実装がわからない時はPAST本を頼りに実装していました。特に実装面で困ったことはないので、これで勉強しながら解き進めるのが良い気がしています。この本はめちゃめちゃコードが読みやすくて勉強になります。おすすめです。

アルゴリズム実技検定 公式テキスト[エントリー~中級編] (Compass Booksシリーズ)

アルゴリズム実技検定 公式テキスト[エントリー~中級編] (Compass Booksシリーズ)

Amazon

今後について

AtCoderを始めたばかりの3年前からずっと水色（Rating1200）になるのが目標なのでゆっくりですが継続して勉強していきたいです。色々な都合でコンテストには出られないことが多いんですが、勉強を継続していれば少しずつ自分の実力が上がってきて将来のコンテストでいい結果を残せると信じて、今後も引退しないように少しずつ継続して勉強していきたいです。水色になれるまでやめなければ水色にはなれると思っています。

今後は蟻本での勉強を考えています。これはかなり難しくハードルが高いのですが少しずつ継続して頑張ります。

 

プログラミングコンテストチャレンジブック [第2版]　～問題解決のアルゴリズム活用力とコーディングテクニックを鍛える～

プログラミングコンテストチャレンジブック [第2版]　～問題解決のアルゴリズム活用力とコーディングテクニックを鍛える～

Amazon

 

【Part7】統計検定準1級：時系列解析のまとめ【ダービン・ワトソン比】

統計検定

1. はじめに

本記事は統計検定準1級の時系列解析分野の一歩目を高校数学レベルから丁寧に解説してみようという趣旨です。対象は統計検定2級を取ったくらいの方から準1級の入り口で悩んでる方くらいが主な想定です。

今回は統計検定頻出のダービン・ワトソン検定、ダービン・ワトソン比について扱っていきます。

前回までの記事はこちらです。
【Part1】統計検定準1級 時系列解析のまとめ【過去問の分析・出題内容・勉強法】 - Syleir’s note
【Part2】統計検定準1級 時系列解析のまとめ【自己相関係数・定常性】 - Syleir’s note
【Part3】統計検定準1級 時系列解析のまとめ【統計モデリング・ホワイトノイズ】 - Syleir’s note
【Part4】統計検定準1級：時系列解析のまとめ【AR過程】 - Syleir’s note
【Part5】統計検定準1級：時系列解析のまとめ【MA過程】 - Syleir’s note
【Part6】統計検定準1級：時系列解析のまとめ【スペクトル密度関数・スペクトラム】 - Syleir’s note

一記事取っておいてなんですが、最近はダービンワトソン比はあまり出題されません。
邪推としては、ダービンワトソン比にはさまざまな問題点が指摘されているため統計学会としても出題しづらくなってしまったのでしょうか。
ただCBTでは出題される可能性があるため一応扱っておきます。

2. ダービンワトソン比って何に使うの？

重回帰分析において重回帰モデルの誤差項が自己相関、系列相関があるかを推定するのに使います。
時間tにおける重回帰モデルの誤差項U_{t}が、AR(1)モデルに従うとき、
U_{t} = \rho U_{t - 1} + \epsilon_{t}と表せます。

自己相関がないとき、U_{t}はU_{t-1}の影響を受けないので\rho = 0となります。
逆に、自己相関があるとき、\rho \neq 0 となります。

ということで、誤差項がAR(1)モデルに従うと仮定したときに誤差項が自己相関を持つかどうかの検定をダービンワトソン検定といいますが、これは\rho = 0 vs \rho \neq 0 の検定をしていることになります。

3.使用する統計量

ダービンワトソン検定においても一般のT検定、F検定などと同じように帰無仮説に基づく、検定統計量を設定し、それが実際の実現値と照らしてどうかという検定になります。
例えばt検定では帰無仮説 \mu = \mu_0の下で、検定統計量 T = \dfrac{\overline{X} - \mu_{0}}{s /\sqrt{n}}が自由度n-1のt分布の中でどうなるかという評価をして帰無仮説を棄却するかの検定を行いました。

同じようにダービンワトソン検定においても、帰無仮説\rho = 0の下で検定統計量 DW = \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t} - \hat{U}_{t-1} )^2}{\sum_{t=1}^{T} \hat{U}_{t}^2}が2に近いかどうかという評価をして検定することになります。

なお、この DW = \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t} - \hat{U}_{t-1} )^2}{\sum_{t=1}^{T} \hat{U}_{t}^2}をダービンワトソン統計量と言います。

4. DW統計量を変形してみる

自分はこの変形を統計検定の記述問題対策で空でできるようにしていましたが、今はCBTなので、結果だけをふんふん言って学んでもらえれば大丈夫です。
DW = \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t} - \hat{U}_{t-1} )^2}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t}^2 - 2 \hat{U}_{t} \hat{U}_{t-1} + \hat{U}_{t-1}^2)}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t}^2 + \hat{U}_{t-1}^2 - 2 \hat{U}_{t} \hat{U}_{t-1})}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{\sum_{t = 2}^{T} \hat{U}_{t}^2 + \sum_{t = 2}^{T} \hat{U}_{t-1}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{\sum_{t = 2}^{T} \hat{U}_{t}^2 + \sum_{t = 1}^{T - 1} \hat{U}_{t}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{\sum_{t = 1}^{T} \hat{U}_{t}^2 - \hat{U}_{1}^2 + \sum_{t = 1}^{T} \hat{U}_{t}^2 - \hat{U}_{T}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{\sum_{t = 1}^{T} \hat{U}_{t}^2+ \sum_{t = 1}^{T} \hat{U}_{t}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{1}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{T}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2}
= \dfrac{2( \sum_{t = 1}^{T} \hat{U}_{t}^2 - \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1})}{\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{1}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{T}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2}

ここで、時系列が十分に長い（ T >> 0）とき、 \sum_{t=1}^{T} \hat{U}_{t}^2 >> \hat{U}_{1}^2, \hat{U}_{T}^2だから、
\dfrac{ \hat{U}_{1}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2} \fallingdotseq 0 , \dfrac{ \hat{U}_{T}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2}\fallingdotseq 0であり、

\fallingdotseq \dfrac{2( \sum_{t = 1}^{T} \hat{U}_{t}^2 - \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1})}{\sum_{t=1}^{T} \hat{U}_{t}^2}
= 2(1 - \dfrac{ \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2} )
= 2(1 - \hat{\gamma}_{1})


となる。ただし \hat{\gamma}_{1}は1次の自己相関係数\rhoの推定量である。

5. DW比と自己相関係数の関係

さて、式変形が終わったところで、オイシイとこだけを取って結果だけを眺めます。
DW \fallingdotseq 2(1 - \hat{\gamma}_{1})
ですね。
ここから、
\rho = 0 \iff \hat{\gamma}_{1} = 0 \iff DW = 2
\rho > 0 \iff \hat{\gamma}_{1} > 0 \iff DW < 2
\rho < 0 \iff \hat{\gamma}_{1} < 0 \iff DW > 2
が言えます。

結果として、これを日本語で書くと、
DW比が2に近いか否かで簡便に自己相関があるかというのが判別できることになります。
なお \rho と 0 の大小関係とDWと 2 の大小関係は反転しているので気をつけましょう。

6.終わりに

ここでPart1の記事を引用します。

過去問を分析した結果、特に手厚い出題がある分野は
自己共分散関数、自己相関関数、ARモデル、MAモデル、コレログラム、スペクトル密度関数、DW統計量になります。

どうですか。一応網羅的に触れられたと思っています。過去問のカバー率はこの記事群で9割近くあります。（当社調べ）。ワークブックと並行しながら概念理解ができたらいいなの気持ちで書き始めましたが記事単独でも意外と網羅率が高くなってよかったです。

とりあえず、統計検定準１級、時系列対策の本編としてのシリーズは終了です。書くのが遅くて完走まで5ヶ月かかってしまいました。ごめんなさい。まあまあ努力を必要とする割に反響が少なくていまいち需要があるのかわからないので、感想とかあればお気軽にくれると他のトピックで同じことをやる気力が湧くかもしれません。時系列解析の入口に入るお手伝いができていたら嬉しいですね。一緒に沼へ入りましょう。

【Part6】統計検定準1級：時系列解析のまとめ【スペクトル密度関数・スペクトラム】

統計検定

1. はじめに

本記事は統計検定準1級の時系列解析分野の一歩目を高校数学レベルから丁寧に解説してみようという趣旨です。対象は統計検定2級を取ったくらいの方から準1級の入り口で悩んでる方くらいが主な想定です。

今回は統計検定頻出のスペクトル密度関数・スペクトラムについて扱っていきます。

前回までの記事はこちらです。
syleir.hatenablog.com
syleir.hatenablog.com
syleir.hatenablog.com
syleir.hatenablog.com
syleir.hatenablog.com

2. 周波数解析について

突然ですが、次のグラフの周期はいくつでしょうか。

もちろん1ですね。

次のグラフの周期はいくつでしょうか。

もちろん2ですね。これもわかりやすいです。

周期とはなんでしょうか。
関数 f が周期 P を持つとは、
任意のxに対して f(x+P)=f(x)が成立することを言います。見かけでもかなりわかりやすいですね。

では周期を持つ２つのグラフを合成するとどうなるでしょうか。

たった2つのグラフの合成ですが、非常に直感的ではなくなってしまいました。よく観察すれば周期1のグラフと周期2のグラフの合成であることがわかりますが、少し時間がかかります。これが個数が増えたらもっと大変になるのはいうまでもありません。でも世の中には周期関数の重ね合わせでできているグラフがどのような周波数の関数の合成でできているのかを知りたいことって結構あると思います。どうですか？

例えば自分がお店を経営していて、店舗の売上のグラフを見て、
・1年ごとの周期があるか、曜日ごとに特徴があるか、月レベルでは何日にピークがあるのか

って知りたくなりませんか？周期というのは時系列解析における重要なモチベーションになっていることがわかります。

3. では具体的にどのように調べればいいのか？

→フーリエ変換というものをすれば良いです。現実的には離散データしか取ってこれないので、これをサンプリングして集めてきて、フーリエ変換というものをすると、どのような周波数成分を持っているのかを調べることができます。これには計算の高速化のテクニックがありますが、今回は割愛して結果だけ示します。先程の例だとこうです。

対数表示してしまっているのでわかりにくいですが、ピークが0.5と1のところに現れているのがわかります。周波数成分の合成のものに対してフーリエ変換をするとピークとして周波数成分が現れることがわかります。

4. スペクトル密度関数とは？

めちゃくちゃざっくりいうと自己共分散関数のフーリエ変換です。スペクトラムともいいます。

...これで通じてくださる読者の方はブラウザバックして良いのでこれを解説していこうと思います。


ラグが大きくなると自己共分散\gamma_hが急速に減衰し、
\sum_{- \infty}^\infty |\gamma_h| < \infty を満たすとき、 \gamma_hに対してフーリエ変換をすることができます。
その結果がこれです。導出はレベルを逸脱するので省略します。
f(\lambda) = \frac{1}{2 \pi} \sum_{- \infty}^\infty \gamma_h e ^{-i \lambda h}で定義されますが今回はお気持ちの説明なのであまり使いません。

これは自己共分散のフーリエ変換で、フーリエ変換とは元の関数の周期がどのようなものでできているのかを調べる手法でしたから、スペクトル密度関数を作って、グラフを書くことで自己共分散の周波数成分がわかるというのがミソです。

スペクトル密度関数における「高さ」はその周波数領域の成分が多いということを意味します。ただ、実際の時系列モデルから作ったスペクトル密度関数では先程みたいに明らかなピークを持って現れるというわけではありません。滑らかなグラフになることも多いです。この考え方をここから示していきます。

5. スペクトラムと自己共分散関数の関係

例えば、次のようなスペクトル密度関数が得られた場合を考えてみましょう。

この場合、低周波領域が強く出ており、高周波領域が弱く出ていることがわかります。ということは、自己共分散関数が低周波成分が多いということになります。低周波が多いということは、よりゆっくり振動するということで、自己共分散関数（Part2参照）で表すと滑らかなグラフになることになります。
逆にスペクトラムで高周波領域が強いグラフの場合、自己共分散関数だと「ギザギザな」グラフになることがわかります。

今の議論をまとめると、
・スペクトラムで低周波が強い→自己共分散関数は滑らか
・スペクトラムで高周波が強い→自己共分散関数はギザギザ
ということになります。

より具体的に説明するために、
ここで、2つのAR(1)モデルを用意します。
Y_{t} = 0.5 Y_{t-1} + \epsilon_t

Y_{t} = -0.5 Y_{t-1} + \epsilon_t

これらの自己共分散関数の推定値であるコレログラムは以下のようになります。
Y_{t} = 0.5 Y_{t-1} + \epsilon_t

Y_{t} = -0.5 Y_{t-1} + \epsilon_t


これから、自己共分散関数とスペクトラムの関係がわかります。
上の方が自己共分散関数が滑らかなのでスペクトラムでは低周波が強い
下の方が自己共分散関数がギザギザなのでスペクトラムでは高周波が強い
と推測できます。実は上に出したスペクトラムは Y_{t} = 0.5 Y_{t-1} + \epsilon_tのものです。


この項で大事なのは関数モデル↔︎自己共分散関数↔︎スペクトラムを自在に行き来できるようになることにあります。
時系列データとスペクトラムを2セットずつ与えられたときに、どちらのグラフがどちらのスペクトラムと対応するかが考えられるのが大事で、コレも過去に何度か出題されている事項です。

6. ペリオドグラムについて

スペクトラムは自己共分散の式から計算によって導出されるものです。
実際の解析には、実際のデータしかなく、自己共分散の式はわかりません。計算方法は割愛しますが、実際のデータから計算する近似的なスペクトラムをペリオドグラム（ピリオドグラム）といいます。ペリオドグラムから、実際のスペクトラムがどのようなものかを推測する、という運用を実世界ではやっています。これも過去に出題がありますが、グラフの見方はスペクトラムと同じなので、良く考えて解答すると良いでしょう。

実際のデータ↔︎コレログラム↔︎ペリオドグラム
関数モデル↔︎自己共分散関数↔︎スペクトラム
とそれぞれ対応します。

7.終わりに

本日の記事ではスペクトル密度関数について解説しました。フーリエ変換の気持ち、すこしはわかっていただけましたか？ここは自分も勉強していて困ったところなので、はじめの一歩として、何がモチベーションなのか、どういうことをしたい操作なのか、伝わると嬉しいです。次回は時系列シリーズ最後になりますが、ダービンワトソン比（DW比）について扱います。（最近は統計検定で出題されていませんが。）
syleir.hatenablog.com

関連記事

syleir.hatenablog.com

この記事にいただいたコメントの回答記事です。本記事で扱わなかったMA(1)モデルのスペクトラムについて扱っています。かなり詳細に解説したつもりなのでこちらもぜひ。

【Part5】統計検定準1級：時系列解析のまとめ【MA過程】

統計検定

1. はじめに

本記事は統計検定準1級の時系列解析分野の一歩目を高校数学レベルから丁寧に解説してみようという趣旨です。対象は統計検定2級を取ったくらいの方から準1級の入り口で悩んでる方くらいが主な想定です。
さて、前回は、AR過程について勉強しました。今回はAR過程についで時系列分野における主要な統計モデルの双璧、MA過程について触れていきます。

前回までの記事はこちらです。
syleir.hatenablog.com
syleir.hatenablog.com
syleir.hatenablog.com
syleir.hatenablog.com





2. 移動平均過程（MA過程）のお気持ち

移動平均過程とは過去のノイズの影響がある程度現在の値Y_{t}に影響を与えているというモデルです。過去直近のq個のノイズが現在値に影響を与えているとき、それを明示してMA(q)モデルと書きます。ARモデルが直近過去数個の実際の時系列データが次の時系列データに影響を与えているというモデルなのに対して、MRモデルは直近n個のノイズがそれぞれ影響して次の時系列データを形成しているという考え方をします。潜在因子を仮定したりするときのモデリングで都合が良いです。

MAモデルの概念図

2.1. 定義

q次の移動平均過程とはY_{t}が連続した直前q個までの\epsilon_{t}, \epsilon_{t-1}, ... \epsilon_{t-q}で説明され、
Y_{t} = \mu +\epsilon_{t} + \theta_{1} \epsilon_{t-1} + ... + \theta_{q} \epsilon_{t-q}
で表されるものをいう。。各\epsilonは現在の値に影響を与えているノイズ、各\thetaはそれぞれのノイズが現在の時系列データにどの程度の影響を与えているかを考える係数。\muは定数項である。

さて、MA(q)モデルを書いてみたものの、統計検定上はなかなか出題されないことと、今回の記事の趣旨は初学者向けの記事ということもあり、より簡単なMA(1)モデルから説明をしようと思います。MA(1)モデルはMA(q)モデルのq=1の場合と考えることで同様に考えることができ、

2.2. 定義(MA(1)モデル)

1次の移動平均過程(MA(1)過程)とは、Y_{t}が今のノイズ\epsilon_{t}と直前のノイズ\epsilon_{t-1}で説明され、
Y_{t} = \mu +\epsilon_{t} + \theta_{1} \epsilon_{t-1}
で表されるものをいう。 \theta_{1} は直前のノイズにどの程度の影響を受けているのかを考える係数。
というように定義することができます。ここでは \epsilonにホワイトノイズを仮定することにします。

概念図としては以下の通りで、現在の時系列データが今現在のノイズと直近のノイズに直接の、そして最大の影響を受けていることがわかります。

2.3 \theta_{1}を変えて色々見てみよう

MR(1)モデルの係数を色々変更して挙動を見てみましょうか。 t = 0 から t = 49 まで50個データを出して見てみます。

2.3.1 \theta_{1} = 0.2


2.3.2 \theta_{1} = 1.2


2.3.3 \theta_{1} = 1000


どうでしょうか。スケール自体は変わっている気がしますが概形は同じではないでしょうか。ざっくり言うと、MA過程における\thetaにはスケール調整の役割があることがわかります。
また、どうして概形が同じに見えるのでしょうか。実はMA(1)過程は共分散定常（弱定常）であることが知られています。Part2の記事でも解説しましたが、共分散定常には平均・分散：tにもhにもよらず一定、自己共分散、自己相関係数：tによらずhにのみ依存するという性質があり、これらの性質、特に平均と分散が一定という性質により概形が似て見えるのです。

この常にMR(1)過程が共分散定常という性質はAR(1)過程の|\phi_{1}| < 1 と |\phi_{1}| \geqq 1で定常性が変わるというところと明確に区別される性質なのでとても重要です。


3. 共分散定常性を示す

さて、ここから共分散定常性を示しに行きましょう。
共分散定常の定義は平均と自己共分散がラグの大きさのみに依存し t に依存していないことでありました。これを示します。

3.1MA(1)過程の期待値

ホワイトノイズの期待値は0なので、\epsilonの期待値は0になります。
Y_{t} = \mu +\epsilon_{t} + \theta_{1} \epsilon_{t-1} この式の両辺の期待値を取ると、
E[Y_{t}] = \mu
となり事実、tによらず一定値をとることがわかります。

3.2MA(1)過程の分散と自己共分散

分散については、求める分散を\gamma_{0}とすると、
\gamma_{0}= E[(Y_{t} - \mu) ^ 2]
= E[(\epsilon_{t} + \theta_{1} \epsilon_{t-1})^2 )]
= E[\epsilon_{t}^2 + 2 \theta_{1} \epsilon_{t} \epsilon_{t-1} + \theta_{1} ^ 2 \epsilon_{t-1}^2) ]

ホワイトノイズ\epsilonは分散\sigmaで自己共分散0のものを仮定することが多く、それを援用すると、

= \sigma ^ 2 + \theta_{1} ^ 2 \sigma ^ 2
= (1 + \theta_{1} ^ 2) \sigma ^2
となり、tに依存しないことがわかる。

1次の自己共分散については、求める自己共分散を\gamma_{1}とすると、
\gamma_{1}= E[(Y_t - \mu)(Y_{t - 1} - \mu)]
= E[(\epsilon_t + \theta_{1} \epsilon_{t - 1})(\epsilon_{t - 1} + \theta_{1} \epsilon_{t - 2} )]
ホワイトノイズ\epsilonは分散\sigmaで自己共分散0だったから、 E[\epsilon_{t - 1}^2 ]以外の項は0で、

= \theta _{1} \sigma ^ 2

となる。

2次以上の自己共分散についてはラグh(>0)として、
\gamma_{h}= E[(Y_t - \mu)(Y_{t - h} - \mu)]
= E[(\epsilon_t + \theta_{1} \epsilon_{t - 1})(\epsilon_{t - h} + \theta_{1} \epsilon_{t - h - 1} ) ]

ここで、t, t - 1,t - h, t - h - 1は全て相異なるから、

= 0 となる。
以上より、自己共分散においても、t に依存していないことがわかり、共分散定常が示される。

3.3 MA(q)過程の共分散定常性

より一般にMA(q)過程の共分散定常性についても同様に示すことができる。ワークブックに計算結果があり、実際に定義通り計算するとできるのでやってみてほしい。（需要があれば追記します。）

4.終わりに

ここで、時系列モデルの双璧、ARモデル、MAモデルの説明が終わりました。次回はスペクトル密度関数について扱いたいと思います。更新時期についてはやる気次第です。目標は1ヶ月以内の執筆です。気長にお待ちください。

→即日執筆しました。えらい。
syleir.hatenablog.com

統計的因果推論のお気持ちを書く

はじめに&お詫び

現実が忙しすぎて投稿が滞っています。本当に少しですが記事の執筆も進めていますので気長にお待ちください。記事を書いているうちに統計的因果推論について書きたいことが増えてきましたのでまずお気持ちの説明だけしておこうと思ってここに書いておきます。統計検定にはあまり出ない部分ですが実用上よく使うのでぜひ。

 

統計的因果推論って何がしたいの？

統計学的に因果関係を示したい。以上です。

本日のブログはこれで終わりです。

統計学のモチベーションには色々なものがあり、例えば関連の探索（どの変数が結果に効いているのか）、予測（株価の予測、将来人口の予測）など色々なモチベーションがあります。これらのモチベーションの中に因果関係を示したいというものがあります。それを実現するための道具が統計的因果推論になります。

 

 

因果関係ってそもそもなんだっけ？

原因と結果の関係のことです。事象Aが事象Bに先行して発生し、事象Aが発生するか否かで事象Bが発生するかが変化するとき因果関係があるといいます。

因果関係を調べるにはどうしたらいいの？

全く同じ状況に対して、原因となる介入をする場合、しない場合で結果がどうなるかを比較すればいいです。簡単ですね。

 

昔々、僕はコーラを飲んだら歯が溶けますよって言われました。でも逆張りの幼少期ぼくはコーラを飲んでも歯が溶けないと思っていました。この因果関係があるかを検証するにはどうしたらいいでしょうか。コーラを飲んだ場合とコーラを飲まない場合を比較してぼくの歯の溶け方を比較すればいいです。

違う例を出しましょう。風が吹けば桶屋が儲かるということわざがあります。果たして本当でしょうか。全く同じ日に、同じ店で、風を吹かせる場合と吹かせない場合で桶屋の売り上げを比較すればいいです。

これらの場合、コーラを飲んでいた方が歯が溶けていたらそれはコーラを飲んだら歯が溶けるということが言えます。また風を吹かせた方が桶屋が儲かっていたら風が吹けば桶屋が儲かるということが言えます。

このようにして、因果推論の基本は、

①因果関係の仮説を立てる
②原因が何かを定義する
③結果が何かを定義する
④検証する

というような手順で考えることができます。

 

因果推論の何が難しいの？

これに関しては圧倒的に④検証するです。コーラを飲んで歯が溶けるか検証する例では、全く同じ条件下でコーラを飲んだ世界線とコーラを飲んでいない世界線を用意して比較検証しなくてはいけません。なぜなら、コーラを飲んだ、飲んでいない以外の条件が揃っていないと、その影響が因果関係に影響を与えているかもしれないからです。

例えば、AくんとBくんを用意して、Aくんにはコーラを飲ませる、Bくんにはコーラを飲ませないという条件設定をして、歯が溶けるか比較検討した際、たとえ歯の溶け方が異なっていても、個人差が影響を与えている可能性があるからです。現実的に、同一人物が同一条件下でコーラを飲みながらコーラを飲まないということはできません。これが因果推論の難しいところになります。

実際に同一条件下で比較することはできません。コーラを飲んだ場合と飲んでいない場合、同時に比較できないことから実際に行った方を事実、行っていない方を反事実と呼んだりします。統計的因果推論では実際に作り得ない反事実をどうやって近似するかということに多大な労力を費やしていて、これが統計的因果推論のお気持ちです。

実際に統計的因果推論をするときはどうするの？

個人レベルでは同一条件下に事実と反事実を同時に実現することができないから因果推論は難しいという話をしました。

なので、実際に仮説を検証する際は集団レベルでの検証を行います。ランダム化比較試験などを行うことが多いです。臨床研究などでランダム化比較試験が往々にして使われるのはこれが理由です。現実世界には反事実を生成できる「もしもボックス」が存在しないのでこういう周りくどいことをするわけですね。もしもボックスがあれば色々な研究ははちゃめちゃに進むと思いませんか？

最近、ランダム化比較試験は臨床研究のみならず、色々なA/Bテストを初め、分野を超えて活用されています。環境分野で使われてるのが最近のトレンドでしょうか。2019年のノーベル経済学賞なんかはこのモデルが使われていますね。以下の2冊は上記ノーベル賞研究者の著書です。臨床研究を超えた因果推論の話として読み物として非常に面白いので読んでみてください。

 

政策評価のための因果関係の見つけ方 ランダム化比較試験入門

政策評価のための因果関係の見つけ方 ランダム化比較試験入門

Amazon

 

貧乏人の経済学――もういちど貧困問題を根っこから考える

貧乏人の経済学――もういちど貧困問題を根っこから考える

Amazon

 

 

 

 

 

 

 

【読書記録】1月, 2月に勉強したことを振り返る

1月は忙しくあまり勉強できなかったので2ヶ月まとめてのお届けです。

前回の記事はこちら。

 

syleir.hatenablog.com

 

1. アルゴリズム実技検定公式テキスト

アルゴリズム実技検定 公式テキスト[エントリー~中級編] (Compass Booksシリーズ)

アルゴリズム実技検定 公式テキスト[エントリー~中級編] (Compass Booksシリーズ)

Amazon

2日かけて一通りやりました。めちゃくちゃ勉強になりました。Python本職じゃない人が書いているのでコンテストにありがちな呪文みたいな実装じゃなくてわかりやすいのがめちゃ良かったです。

他の本だと知らないアルゴリズムがC++ で実装されてたりしてやる気をなくすことが多かったのですが、Pythonネイティブで書かれているのでストレスフリーで読めてサクサク読み進めることができました。Pythonistaさんには非常におすすめです。来月はデータ構造の管理あたりを勉強したいと思っています。

 

syleir.hatenablog.com

この記事に抱負を書きましたが、AtCoderはこれから少しずつ頑張りたいと思っています。

2. A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは

 

A/Bテスト実践ガイド　真のデータドリブンへ至る信用できる実験とは (アスキードワンゴ)

A/Bテスト実践ガイド　真のデータドリブンへ至る信用できる実験とは (アスキードワンゴ)

Amazon

この本はオンラインでの対照実験についての本です。A/Bテストとは、Web広告などを最適化するための方策で、AパターンとBパターンを用意して、それぞれで実験を行い、どれくらいの効果があるかや、どちらが優れているかを評価する方法です。例えば、この記事を書いたあとで、twitterに記事を書いたことをお知らせするAパターンと、お知らせしないBパターンとで、どれくらい集客に差が生まれるかを知りたいときなどに利用することができます。

この本の良いところは陥りやすいピットフォールを列挙してくれるところです。人は失敗から学ぶことが多いとは言いますが、統計手法自体の失敗はなかなか気づくことができないので、A/Bテストにありがちな失敗をあげてくださるのは嬉しいです。また、巨大プラットフォームでのA/Bテストなんかは我々にはできない経験なので、そういうのも書いてくださるのは非常に嬉しいです。貴重な経験です。

余談ですが、この本の誤りを発見したので出版社のドワンゴさんに連絡したらちゃんと中身を検証して丁寧なメールを送ってくださいました。ドワンゴさんにはこれからも素晴らしい書籍を出してくださることを期待しています。

ところで、この本からも新しい学びがあって、先日それをPythonで実装したので今後また記事にしたいと思います。長編になりそうな割に労力だけがかかってかつ集客力のない記事が生まれそうです。やる気をください。

3．現場で使える！NumPyデータ処理入門 機械学習・データサイエンスで役立つ高速処理手法

 

現場で使える！NumPyデータ処理入門 機械学習・データサイエンスで役立つ高速処理手法

現場で使える！NumPyデータ処理入門 機械学習・データサイエンスで役立つ高速処理手法

Amazon

AtCoderではPythonを使っていますがNumPyを使った実装をしたいなって思った時にネット記事より書籍の方が体系的に勉強できるので買いました。一応Numpy自体はE資格でディープラーニングの実装をするときに多用するのである程度知っていましたが競技プログラミング特有のテクニックや高速化の話は全く知らなかったので、とても勉強になっています。自分のレート帯のPythonistaさんではあまりNumPyを使ってる人は見ないですが、線形代数的手法や統計学的手法を必要とするテクニックや、並列操作、ブロードキャストが使えるのがお手軽で実装量を減らしつつ高速化できるのでおすすめです。NumPy。

 

4. データサイエンティスト入門 (日経文庫)

データサイエンティスト入門 (日経文庫)

データサイエンティスト入門 (日経文庫)

Amazon

一般的なデータサイエンティストになる気はそんなにないのですが、自分のやっていることがどのような仕事に繋がるのか、またその分野ではどのようなことが前提知識となっているのかを知りたくて買いました。この本の中では統計検定がおすすめされてて笑いました。統計検定、役に立ちますよ。取りましょう（宣伝）。

 

 

syleir.hatenablog.com

終わりに

全体的に１月２月は競技プログラミングにシフトを置いた生活をしていました。長く楽しめる趣味として今後も続けていきたいのですが、なかなか勉強時間をまとまって取れない生活になってくると思うので少しずつ進めたいと思っています。

来月は少し統計寄りの記事を書けたらいいなと思っています。ちょっとずつ執筆中です。