1. はじめに
本記事は統計検定準1級の時系列解析分野の一歩目を高校数学レベルから丁寧に解説してみようという趣旨です。対象は統計検定2級を取ったくらいの方から準1級の入り口で悩んでる方くらいが主な想定です。
さて、前回は、ホワイトノイズと統計モデリングについて勉強しました。今回は時系列分野における主要な統計モデル、AR過程について触れていきます。
前回までの記事はこちらです。
syleir.hatenablog.com
syleir.hatenablog.com
syleir.hatenablog.com
2. 自己回帰過程(AR過程)
自己回帰過程というのは隣り合ったいくつかの過程について、その値が同じような値が出るのか、違った値が出やすいのかを定式化したモデルです。直前のデータの影響を受けて時系列データが生成されていると考えるモデルをAR(1)モデルと言います。直前の連続したp個のデータの影響を受けて時系列データが生成されていると考えるモデルをAR(p)モデルと言います。このpを次数ということもあります。さて、このAR(p)モデルを定式化することを考えます。
2.1. 定義
p次の自己回帰過程とはが連続した直前p個までの
で説明され、
で表されるものをいう。各はそれぞれがどの程度の影響を受けているのかを考える係数で、最後の
は誤差である。ホワイトノイズを採用することが多い。cは定数項である。
さて、AR(p)モデルを書いてみたものの、統計検定上はなかなか出題されないことと、今回の記事の趣旨は初学者向けの記事ということもあり、より簡単なAR(1)モデルから説明をしようと思います。AR(1)モデルはAR(p)モデルのの場合と考えることで同様に考えることができ、
2.2. 定義(AR(1)モデル)
1次の自己回帰過程(AR(1)過程)とは、が直前の
で説明され、
で表されるものをいう。 は直前の時系列データにどの程度の影響を受けているのかを考える係数で、最後の
は誤差である。ホワイトノイズを採用することが多い。
は定数項である。
というように定義することができます。ここでは にホワイトノイズを仮定することにします。
2.3  を変えて色々見てみよう
を変えて色々見てみよう
さて、AR(1)モデルは経験上係数を色々変更して挙動を見てみるのが一番わかりやすいです。
以降では簡単のため と固定して
から
まで50個データを出して見てみます。
2.3.1 

2.3.2 

2.3.3 
の場合は
は
となります。
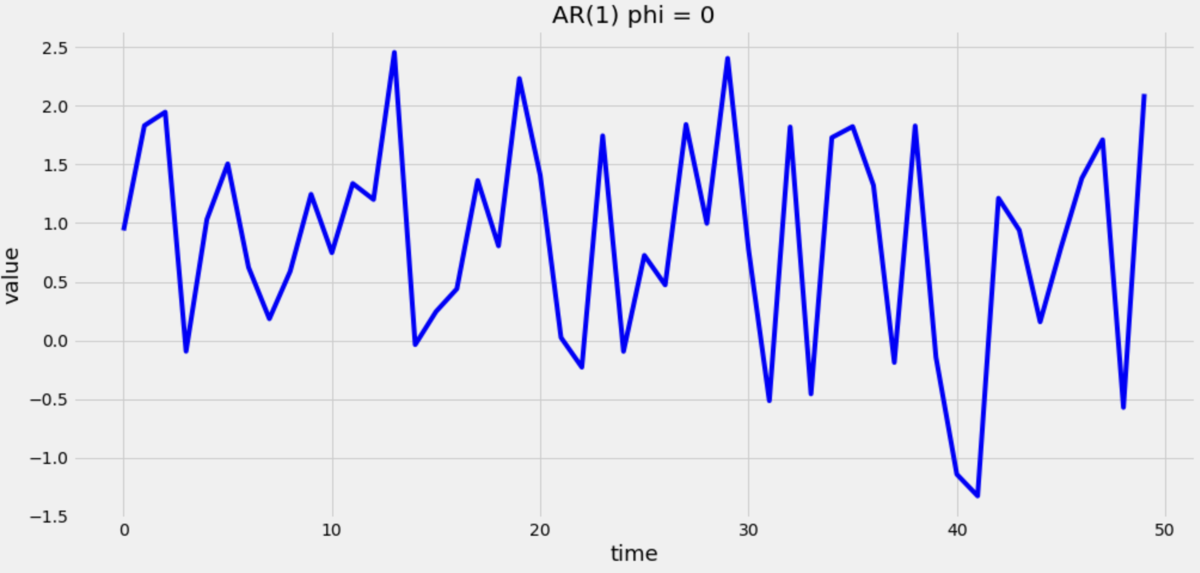
これは前回記事【Part3】統計検定準1級 時系列解析のまとめ【統計モデリング・ホワイトノイズ】 - Syleir’s note
で紹介したホワイトノイズを +1 平行移動させたものになります。
2.3.4 

2.3.5 

どうでしょうか。 が減少するにつれてグラフの「滑らか度合い」が減っているような気がしませんか? AR(1)の式
を見てもらえれば分かりますが、
は
がどれだけ次の時系列である
に影響を与えるかのパラメータとなっています。
が大きいときは
と
とが同じ値を取りやすくなり、
でちょうど
と
とが完全にランダム、
が負のときは
と
とが正負逆の値を取りやすくなる、というようなことが言えます。
このグラフを見て、 がどれくらいかを定性的に見積もるというのは過去問でも出題されているのでできるようになるといいでしょう。手元環境で上記の時系列データが出力できるようにするようなコードもいつか公開するつもりではあります。
2.4  をさらに変えてみよう
をさらに変えてみよう
さて、上の項ではあえて、 の動く範囲に制限を与えてグラフを描写していました。本項ではその制限を取り払ってみようと思います。
2.4.1 

のとき、
は
となります。
に 1 を足してランダムノイズを乗せると
になることから、大体
が1増加すると
も1増加するような挙動をしていることがわかり、これはおおよそ
のようなグラフになります。
ちなみに の時のこの過程をブラウン運動と言います。確率過程における重要な概念ですが脱線してしまうので紹介に留めておきます。
2.4.2 
 ]
]
のグラフはさらに強烈です。これは指数関数のような挙動をしており、
は
で
まで増加しています。ここまで大きくなるとホワイトノイズはカスみたいなものになるので、ぱっと見はとても滑らかなグラフになります。ここから学べることは、鬱陶しい存在がいたとしてもそれより指数オーダーで大きくなれば無効化できるということです。ビッグになりましょう。(違う)
2.4.3 

トランペットみたいで可愛いですね。これもオーダーに比べてカスみたいなホワイトノイズが乗っているので綺麗なグラフに見えますね。
3.  と
と  の決定的な違いとは?
の決定的な違いとは?
前2項であえて分けてグラフを書いたのには、 と
という違いがあるからでした。これがAR(1)モデルにおいては天と地、月とすっぽん、現役と浪人ほど違ってきます。
実際に何が違うのかというと、 では弱定常性(共分散定常性)があるということです。定常性に関してはこの記事のPart2で触れているので参考にしてください。
syleir.hatenablog.com
この証明は難しいので初学者向けのこの記事では書きません。グラフを見て帰納的に得られる事実として利用します。ARオペレータ、特性方程式などの項目でググると出てくるような気がしています。成書で証明までやってるものは今の所見たことがないです。あったら教えてください。過去にも証明は出ていませんが、特性方程式の利用の問題は出題されています。実際はただの高校数学の問題なので、検定に取り組む上ではそこまで理解する必要はないです。
(共分散)定常性とは、平均、分散がtにもhにもよらず一定で、自己共分散、自己相関係数がtによらずhにのみ依存するというものでした。 の例では平均が一定ではなく、
、
の例では平均はともかくとして明らかに分散が一定ではありません。ということで
ではなんとなく共分散定常性がないことが推察されます。
逆に のグラフたちは平均も分散も時間によらず一定そうで、ぱっと見ではわかりにくいですが、自己共分散、自己相関係数もそこまでは時間に依存して変動してなさそうな印象を受けます。ということで
のAR(1)過程では共分散定常性があるということにします。(実際あります)これがこの後の期待値の計算などに生きてきます。
4. AR(1)過程の期待値
ここで、さきほどの式
を考えます。
両辺の期待値を取ると、
となります。ここで、期待値の線形性を利用して、
とできます。ここで、はホワイトノイズだったから、期待値は0となり、
となります。
ここまでの変形は によらず、行うことができます。
ここで生きてくるのが共分散定常性です。共分散定常性が仮定できるとき、つまりの条件下で、共分散定常の条件である、平均が
によらず一定であるというものを使うことで、
とすることができ、
つまり
となります。
ここにきて の役割がわかるようになり、
は確率過程の期待値を決める役割をしていることもわかります。そしてこの操作が共分散定常性という性質に基づいていることからもPart2で説明した定常性の重要性が少し伝わるかなと思います。
分散についても同様に求められます。余力があれば追記します。今日はこの辺で勘弁してください。この辺の計算はガイドブックが詳しいです。実はAR(1)過程の分散はこの誤差項のホワイトノイズの分散が効いてくるという結果が導けます。誤差項といいつつ、確率過程の分散を決定していると言うのは新鮮じゃないですか?確率過程の誤差項、世間一般の誤差のイメージとは違ってめちゃくちゃ大事です。次回はこのことがわかるMA過程について話していきたいと思います。
次回記事です。
syleir.hatenablog.com