【Part7】統計検定準1級：時系列解析のまとめ【ダービン・ワトソン比】

1. はじめに

本記事は統計検定準1級の時系列解析分野の一歩目を高校数学レベルから丁寧に解説してみようという趣旨です。対象は統計検定2級を取ったくらいの方から準1級の入り口で悩んでる方くらいが主な想定です。

今回は統計検定頻出のダービン・ワトソン検定、ダービン・ワトソン比について扱っていきます。

前回までの記事はこちらです。
【Part1】統計検定準1級時系列解析のまとめ【過去問の分析・出題内容・勉強法】 - Syleir’s note
【Part2】統計検定準1級時系列解析のまとめ【自己相関係数・定常性】 - Syleir’s note
【Part3】統計検定準1級時系列解析のまとめ【統計モデリング・ホワイトノイズ】 - Syleir’s note
【Part4】統計検定準1級：時系列解析のまとめ【AR過程】 - Syleir’s note
【Part5】統計検定準1級：時系列解析のまとめ【MA過程】 - Syleir’s note
【Part6】統計検定準1級：時系列解析のまとめ【スペクトル密度関数・スペクトラム】 - Syleir’s note

一記事取っておいてなんですが、最近はダービンワトソン比はあまり出題されません。
邪推としては、ダービンワトソン比にはさまざまな問題点が指摘されているため統計学会としても出題しづらくなってしまったのでしょうか。
ただCBTでは出題される可能性があるため一応扱っておきます。

2. ダービンワトソン比って何に使うの？

重回帰分析において重回帰モデルの誤差項が自己相関、系列相関があるかを推定するのに使います。
時間 $t$ における重回帰モデルの誤差項 $U_{t}$ が、AR(1)モデルに従うとき、
$U_{t} = \rho U_{t - 1} + \epsilon_{t}$ と表せます。

自己相関がないとき、 $U_{t}$ は $U_{t-1}$ の影響を受けないので $\rho = 0$ となります。
逆に、自己相関があるとき、 $\rho \neq 0$ となります。

ということで、誤差項がAR(1)モデルに従うと仮定したときに誤差項が自己相関を持つかどうかの検定をダービンワトソン検定といいますが、これは $\rho = 0$ vs $\rho \neq 0$ の検定をしていることになります。

3.使用する統計量

ダービンワトソン検定においても一般のT検定、F検定などと同じように帰無仮説に基づく、検定統計量を設定し、それが実際の実現値と照らしてどうかという検定になります。
例えばt検定では帰無仮説 $\mu = \mu_0$ の下で、検定統計量 $T = \dfrac{\overline{X} - \mu_{0}}{s /\sqrt{n}}$ が自由度n-1のt分布の中でどうなるかという評価をして帰無仮説を棄却するかの検定を行いました。

同じようにダービンワトソン検定においても、帰無仮説 $\rho = 0$ の下で検定統計量 $DW = \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t} - \hat{U}_{t-1} )^2}{\sum_{t=1}^{T} \hat{U}_{t}^2}$ が2に近いかどうかという評価をして検定することになります。

なお、この $DW = \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t} - \hat{U}_{t-1} )^2}{\sum_{t=1}^{T} \hat{U}_{t}^2}$ をダービンワトソン統計量と言います。

4. DW統計量を変形してみる

自分はこの変形を統計検定の記述問題対策で空でできるようにしていましたが、今はCBTなので、結果だけをふんふん言って学んでもらえれば大丈夫です。
$DW = \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t} - \hat{U}_{t-1} )^2}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t}^2 - 2 \hat{U}_{t} \hat{U}_{t-1} + \hat{U}_{t-1}^2)}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{\sum_{t = 2}^{T} (\hat{U}_{t}^2 + \hat{U}_{t-1}^2 - 2 \hat{U}_{t} \hat{U}_{t-1})}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{\sum_{t = 2}^{T} \hat{U}_{t}^2 + \sum_{t = 2}^{T} \hat{U}_{t-1}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{\sum_{t = 2}^{T} \hat{U}_{t}^2 + \sum_{t = 1}^{T - 1} \hat{U}_{t}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{\sum_{t = 1}^{T} \hat{U}_{t}^2 - \hat{U}_{1}^2 + \sum_{t = 1}^{T} \hat{U}_{t}^2 - \hat{U}_{T}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{\sum_{t = 1}^{T} \hat{U}_{t}^2+ \sum_{t = 1}^{T} \hat{U}_{t}^2 - 2 \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{1}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{T}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= \dfrac{2( \sum_{t = 1}^{T} \hat{U}_{t}^2 - \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1})}{\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{1}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2} - \dfrac{ \hat{U}_{T}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2}$

ここで、時系列が十分に長い（ $T >> 0$ ）とき、 $\sum_{t=1}^{T} \hat{U}_{t}^2 >> \hat{U}_{1}^2, \hat{U}_{T}^2$ だから、
$\dfrac{ \hat{U}_{1}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2} \fallingdotseq 0 , \dfrac{ \hat{U}_{T}^2} {\sum_{t=1}^{T} \hat{U}_{t}^2}\fallingdotseq 0$ であり、

$\fallingdotseq \dfrac{2( \sum_{t = 1}^{T} \hat{U}_{t}^2 - \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1})}{\sum_{t=1}^{T} \hat{U}_{t}^2}$
$= 2(1 - \dfrac{ \sum_{t = 2}^{T} \hat{U}_{t} \hat{U}_{t-1}}{\sum_{t=1}^{T} \hat{U}_{t}^2} )$
$= 2(1 - \hat{\gamma}_{1})$

となる。ただし $\hat{\gamma}_{1}$ は1次の自己相関係数 $\rho$ の推定量である。

5. DW比と自己相関係数の関係

さて、式変形が終わったところで、オイシイとこだけを取って結果だけを眺めます。
$DW \fallingdotseq 2(1 - \hat{\gamma}_{1})$
ですね。
ここから、
$\rho = 0 \iff \hat{\gamma}_{1} = 0 \iff DW = 2$
$\rho > 0 \iff \hat{\gamma}_{1} > 0 \iff DW < 2$
$\rho < 0 \iff \hat{\gamma}_{1} < 0 \iff DW > 2$
が言えます。

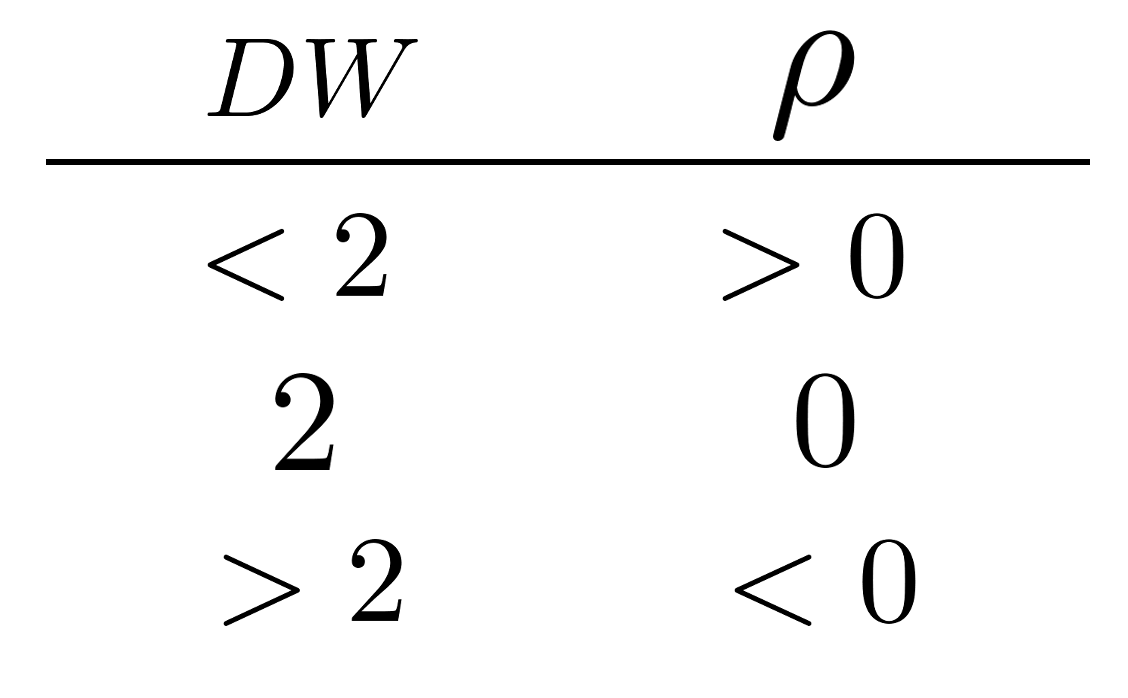
結果として、これを日本語で書くと、
DW比が2に近いか否かで簡便に自己相関があるかというのが判別できることになります。
なお $\rho$ と 0 の大小関係と $DW$ と 2 の大小関係は反転しているので気をつけましょう。

6.終わりに

ここでPart1の記事を引用します。

過去問を分析した結果、特に手厚い出題がある分野は
自己共分散関数、自己相関関数、ARモデル、MAモデル、コレログラム、スペクトル密度関数、DW統計量になります。

どうですか。一応網羅的に触れられたと思っています。過去問のカバー率はこの記事群で9割近くあります。（当社調べ）。ワークブックと並行しながら概念理解ができたらいいなの気持ちで書き始めましたが記事単独でも意外と網羅率が高くなってよかったです。

とりあえず、統計検定準１級、時系列対策の本編としてのシリーズは終了です。書くのが遅くて完走まで5ヶ月かかってしまいました。ごめんなさい。まあまあ努力を必要とする割に反響が少なくていまいち需要があるのかわからないので、感想とかあればお気軽にくれると他のトピックで同じことをやる気力が湧くかもしれません。時系列解析の入口に入るお手伝いができていたら嬉しいですね。一緒に沼へ入りましょう。