【Part2】統計検定準1級時系列解析のまとめ【自己相関係数・定常性】

はじめに

前回は統計検定準1級の時系列解析分野について過去問の分析をしてどういうふうに勉強をしたら良いかを整理しました。
syleir.hatenablog.com
今回からは実際にどういうことを学んでいったらいいか、考え方を含めて整理していきます。
今日の記事では最初に時系列データとは何かという話をして、時系列解析の目標、そして基本統計量と満たしていると嬉しい性質について書きます。

はじめに
1. 時系列データとは？
2. 時系列解析の動機
3. 平均・分散
4. 自己共分散,自己相関係数
5. 定常性
- 弱定常性（共分散定常性）
- 強定常性
6.定常性が仮定できない時はどうするの？
終わりに

1. 時系列データとは？

時間経過を伴いながら観測されるデータのこと。
有名どころだと株価ですかね。

株価も取引ごとに観測されるデータなので時系列データになり得ます。日々の気温なんかも観測していれば時系列データになり得ます。僕は小学生のころ、夏休みの日記で日々の最高気温を1日も記録しなかったので時系列データにはできませんでした。書かれなかったことは、無かったことです。あとはブログのPV数なんかも時系列データになります。

ラーメン屋に並んでる人の人数、アトラクションの待ち時間なんかもいい例かもしれません。最近のトレンドではCovid-19の感染者なんかも1日1回計測される時系列データです。

2. 時系列解析の動機

時系列解析の動機は色々あります。例えば、

この時系列データの特徴を示す量を知りたい。
過去の自分のデータから今の自分のデータがどれくらい影響を受けているかを知りたい。
この時系列データがどのような法則に支配されているのかを知りたい。
どのような周期性があるのかを知りたい。
未来の予測をしたい。
今までの傾向と違うデータを検知したい。

などです。これらの目的に応じた統計的な指標や方法が存在してこれから順番に学んでいくことになります。

3. 平均・分散

時系列分析における平均は時刻 $t$ での期待値を意味します。つまりこの平均値は時刻 $t$ に依存するため、 $\mu_t = E[Y_{t}]$ のように表されます。平易な日本語では「時刻 $t$ のデータはどれくらいになることが見込めるか」です。
同様に分散も時刻　 $t$ での分散を意味します。これも普通の分散と同様に $V[Y_{t} ] = E[(Y_{t} –\mu_{t})^{2}]$ で求めることができます。これの平方根をボラティリティといい、株式投資なんかでは結構メジャーな言葉ですが、「時刻 $t$ におけるデータがどれだけばらつきやすいか」と言い換えることができます。

4. 自己共分散,自己相関係数

自己共分散は元のデータと時間 $h$ ずらしたデータの共分散のことで、
一般の共分散の定義を拡張して
$Cov[t,t-h] = E[(y_t - \mu_t)(y_{t-h} - \mu_{t-h})] = \gamma_{t,h}$
として定義されます。
またこのずらし時間 $h$ のことをラグと言います。

自己相関係数は元のデータと時間 $h$ ずらしたデータの相関係数のことで、
一般の相関係数の定義を拡張して
$\rho[Y_t,Y_{t-h} ] = \frac{Cov[t,t-h]}{\sqrt{V[Y_t]V[Y_{t-h}]}} = \rho_{t, h}$
として定義されます。「元のデータとラグhずらしたデータの値がどれくらい似通っているか」というように言語化することができます。

例えば、周期7で1,2,3,4,3,2,1,1,2,3,4,3,2,1,...を繰り返す以下のような時系列データを考えてみましょう。

・隣同士の時系列データの差分が１ずつしか変動しないのでラグ1の自己相関係数は高そう
・周期が7なのでラグ7の自己相関係数は高そう
・逆に3くらいズレると山と谷でかち合うので自己相関係数が低くなりそう

ということがわかります。
実際に計算してみると、
ラグ1: 0.58998297
ラグ3:-0.8613064
ラグ7:0.92971053

と概ね観察した通りの結果が得られました。

ラグhを横軸、自己相関係数を縦軸として可視化をしてみると

このようになり、ラグ14でも自己相関係数が高いことがわかります。これは周期7の時系列データは周期14の時系列データでもあるからです。
このように自己相関係数を可視化していくことで周期性に気づいたり近接したデータの形の性質に気づいたりすることができるようになります。実はこのグラフをコレログラムといい、統計検定頻出です。

5. 定常性

ここで一息ついて考えると、平均 $\mu_{t} = E[Y_{t}$ ]って不思議な気持ちになりませんか？「時刻 $t$ のデータはどれくらいになることが見込めるか」ってめちゃくちゃ考えるのが難しいですよね。持っているデータは1系列だけで過去のデータしかないのにどうやって任意の時刻 $t$ の期待値 $\mu_{t}$ がわかるんでしょうか。1年後の株価の期待値がそんなに簡単に計算できたら僕は億万長者になれてしまいます。

分散についても同様です。どうやって $V[Y_{t} ] = E[(Y_{t} –$ $\mu_{t}$ $)^{2}]$ を計算したらよいでしょうか。

自己共分散、自己相関係数についても $\mu_{t},\mu_{t-h}$ が含まれます。どうやって計算したらよいでしょうか。案外難しい概念になると思います。例えば株価のボラティリティの計算は直前の数データを引っ張ってきてそれらのデータが同じルールに支配されて動いていると仮定した上でそれらのデータで標準偏差を算出したりしています（ヒストリカルボラティリティ）。

さて、それはさておき、データの分布を見てある仮定が出来れば、これらの計算がめちゃくちゃ楽になります。それが定常性という概念です。定常性というからには何かが常に一定であるということを主張しています。それがなんなのかを見ていきましょう。

弱定常性（共分散定常性）

弱定常性とは平均と共分散が一定であることを主張しています。より厳密には

任意の時間 $t$ ,ラグ $h$ に対して、
$E[Y_t] = \mu$ (一定) $(- \infty < \mu < \infty)$
$Cov[Y_t, Y_{t-h} ] = \gamma_{h}$ ( $t$ によらず一定) $(0 < V[Y_t] = \gamma_{0} < \infty)$ 　

が成立する場合、弱定常と言われます。

これにより、任意の時刻 $t$ での分散は $V_{t} = Cov[Y_t, Y_t ] = \gamma_{0}$ と計算でき、自己相関係数も
$\rho[Y_t,Y_{t-h} ] = \frac{Cov[t,t-h]}{\sqrt{V[Y_t]V[Y_{t-h}]}} = \frac{\gamma_{h}}{\gamma_{0} }= \rho_{h}$
(= 時間 $t$ によらずラグ $h$ にのみ依存する)

この結果をまとめると、弱定常性とは
平均、分散： $t$ にも $h$ にもよらず一定
自己共分散、自己相関係数： $t$ によらず $h$ にのみ依存する
という主張になります。

ファイナンス分野では単に定常性といった場合、この弱定常性をいうことが多いです。

強定常性

強定常性とは任意の整数 $h_1, h_2, ... , h_n$ に対して ${Y_t, Y_{t-h_1},Y_{t-h_2}, ... , Y_{t-h_n}}$ の同時分布が時点tに依存せず、ラグ $h_1, h_2, ... , h_n$ にのみ依存するという主張です。
弱定常性では自己共分散、自己相関係数のみが $t$ によらず $h$ にのみ依存するという主張でしたが、強定常性では全ての構造が $t$ によらず $h$ にのみ依存するという主張であり、より強い主張をしています。強定常というのはこれを反映したネーミングです。

実際、平均と分散が有限であれば、これらの同時分布から自己共分散、自己相関係数が $t$ によらず $h$ にのみ依存するということが言え、この仮定の下で強定常ならば弱定常が示せます。

確率分布が求まれば、（存在すれば　cf. コーシー分布）平均と分散が計算できるように、同時分布が分かれば（存在すれば）自己共分散が計算でき、これらの同時分布がラグにのみ依存していれば計算結果もラグにのみ依存するよ、と解釈しておくのがそれ相応の理解かなと思っています。

まとめると、強定常性とは
同時分布が時点tに依存せず、ラグ $h_1, h_2, ... , h_n$ にのみ依存する
という主張になります。

6.定常性が仮定できない時はどうするの？

定常性は時系列解析分野においてめちゃくちゃ重要というか、これが仮定できないと始まらないくらいの勢いなのでありとあらゆる手段をとって時系列データを調教して定常性を仮定できるようにします。

例えばですが、、先ほどの株価のデータは右肩あがりなので $E[Y_t] = \mu$ (一定) $(- \infty < \mu < \infty)$ が成り立たず弱定常性が怪しいです。

トレンドと移動平均線

ところで右肩あがりであることを示すには何をしたらよいでしょうか。ここで登場するのが移動平均線という概念です。
n日移動平均線は直前n日の平均を取ってそれを新しいデータとしてプロットしていきます。

例えば、3日移動平均線を作りたかったら、1/1-1/3の平均,1/2-1/4の平均,1/3-1/5の平均というように1日ずつずらしてn日分のデータの平均値を描画します。1/1-1/3の平均を何日のデータとしてプロットするかは流派がありますがトレンドを見る上では大差ないのでここでは省略します。

n日移動平均をとるメリットはn日での季節性、周期性を無視したデータが取れます。これにより大域的な挙動、すなわちトレンドが追えるという利点があります。nの決め方は重要です。どのnが一番よいかは統計モデリングによって決定することができます。

例えば先ほどのデータの200日移動平均線を同時に描くとこうなります。

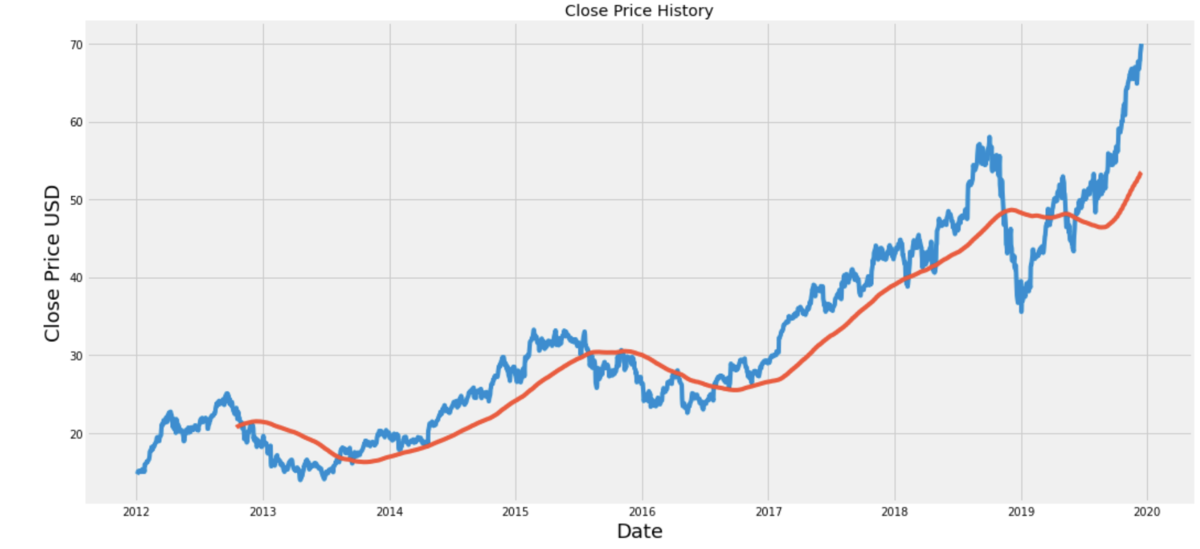
まあトレンドとして右肩あがりと言っていいのではないでしょうか。ということで弱定常性が仮定できません。

階差を取る

そこで時刻 $t$ での株価データを $Y_t$ として階差 $\Delta Y_t = Y_t - Y_{t-1}$ をプロットします。

これにより平均が一定っぽいデータになりました。これは右肩あがりの一次式の微分が一定値になることに起因していたりします。放物線っぽいなというデータには2回階差をとったりします。

分散が一定じゃない時は？

しかし明らかに分散が一定な感じがありません。まだ定常性は言えなさそうですね。こういう時は対数変換をしてお茶を濁したりします。今回は本筋と離れるので書きません。

世の中の大体のデータは非定常

色々なデータが弱定常だったらよいのですが世の中そんなに甘くないです。世の中の関数の多くは積分できないし、世の中の極限は発散しがちだし、世の中の漸化式は解けないものが多いのと同じです。でもあの手この手で弱定常っぽいデータに変換することができます。世の中の時系列予測というのは弱定常であることを前提に作られているものが多いので、我々は必死こいて弱定常っぽく変換できないか？を考える必要があります。本来は。

ということで弱定常というのは非常にありがたい性質なのですが、統計検定においては弱定常だと何が嬉しいのかが省略されて勉強をしてしまいがちです。今後の勉強の際は弱定常に礼拝しながら学習を進めていってください。時系列解析における弱定常は日本人の白米くらい大事です。

終わりに

今日の記事はここまでです。次は時系列解析の統計モデリングのお気持ちについて触れます。この辺から書きだめがないので亀くらい更新速度が遅くなりますがご容赦ください。

次の記事はこちらです。
syleir.hatenablog.com

Syleir’s note

2020.4.1より統計検定やE資格の勉強の進捗を報告しています。統計検定準1級、E資格、G検定取得しました！当ブログへのリンクはご自由にどうぞ。