Syleir’s note

2020.4.1より統計検定やE資格の勉強の進捗を報告しています。統計検定準1級、E資格、G検定取得しました！当ブログへのリンクはご自由にどうぞ。

MENU

target trial emulationの初歩を解説する【統計的因果推論】

統計的因果推論

はじめに

個人的にtarget trial emulationについて勉強する機会があったので備忘録としてもまとめたいと思います。

目次

target trial emulationとは？

横文字は嫌いですが、残念ながら、適切な日本語訳が今のところ存在していない(と思っています)ので、このままtarget trial emulationを使っていきます。

最近激アツのhot topicです。頭痛が痛いみたいですね。
ここ数年で論文投稿数が鰻のぼりに上昇しています。

2024年4月現在の論文投稿数
target trial emulationを読み下すと、 対象となるRCT : randomized controlled trialを明確に定めて(target)、それを観察研究によって模倣(emulation)しようということです。 これを端的に説明するのであれば、「RCTをマネした観察研究を行うことで、制約下でも質の良い研究をしよう」 とする枠組みのこと、ということができるでしょうか。

前提知識

前提知識として、過去記事でも解説した通り、RCTは選択バイアスを減らせる良いデザインです。 syleir.hatenablog.com また、そのほかの想定していない交絡因子も調整してくれる優れものです。実際にRCTと観察研究が結果が食い違っている研究がいくつかありますが、多くの場合はRCTの方がバイアスを低減することができるデザインとされ、信頼性が高く、意思決定に用いられることが多いです。 一方で、RCTには多くの制約があります。
  • ①倫理的制約
RCTには倫理的制約があります。例えば、すでに治療効果がありそうという治療法の研究を行うと、ランダム化で対照群に割り付けられた群が不利益を被るというものや、研究として倫理的制約をはらむものがあります。
  • ②時間的制約
RCTには時間的制約もあります。RCTを行うにはかなりの時間がかかります。これから研究デザインを立てて、承認してもらって、実験して、解析して、という時間を取れないものがあります。研究の期日が決まっているものもありますし、因果推論はなんらかの意思決定のために行いますから、意思決定の期日が迫っていたりするものもあるかもしれません。明日までに治療を行うかを決める時に今からRCTは組めません。
  • ③金銭的制約
そのほか、金銭的制約もあります。治験を組んで、解析を行ってと行っていく時には必ずお金がかかります。治療法によっては莫大なお金が必要です。 そのほかにも、RCTは多くの制約をはらんでいます。このため、RCTをやりたい研究デザインであっても、行えない時があります。target trial emulationはRCTが種々の制約で行えない中で、観察研究をやむを得ず行うときに、より「正しい」結果を出すための枠組みであるとも言えます。

歴史的な流れ

歴史的な流れは理解には不要です。興味がある方だけ読んでください。 これは論文を読んでいる中で当たったもので、成書を当たったわけではないですし、ざっとしか読んでいないので正しさは保証できませんが、大枠の時系列を説明します。 target trial emulationはHarvardのHernánによって発展させられてきた概念です。最初の概念自体はEpidemiology. 2011 May;22(3):290-1.にあり、大規模データベースを用いた観察研究でもRCTと同じような枠組みで考え、CONSORTチェックリスト(RCTの結果を報告するためのチェックリスト)の枠組みで、観察研究でも同じように確認し、どのようにemulateしたか（この論文で実際にemulateという単語が出てきます）を報告する推奨が出されました。これがtarget trial emulationの概念の始まりと思われます。 実際の枠組み、方法論に関しては同じくHernánがAm J Epidemiol. 2016 Apr 15; 183(8): 758–764.の報告で、具体的な「マネ」の仕方を提示してくれました。 教科書では2020年にWhat ifが出版され、この中で取り上げられています。2024年7月に新版が出るようです。 そして、2022年にHernánがJAMA. 2022 Dec 27;328(24):2446-2447.にGuide to Statistics and Methodsとして方法論のガイドとしてのeditorialをCOVID-19に対するトシリズマブでの治療を例に、記載してくれたのでした。そしてJAMAにも載ったことで、一躍価値が認められ、前述したような爆発的な論文数の増加につながっていったのでした。（安易な因果関係の仮定です。） 今回はこれを解説していきます。原著を読みたい方は Target Trial Emulation: A Framework for Causal Inference From Observational Data | Research, Methods, Statistics | JAMA | JAMA Network これを読んでみてください。

target trial emulationの手順

以下、具体的な原著でいうframework:枠組みを解説していきます。

target trial emulationは2ステップからなる

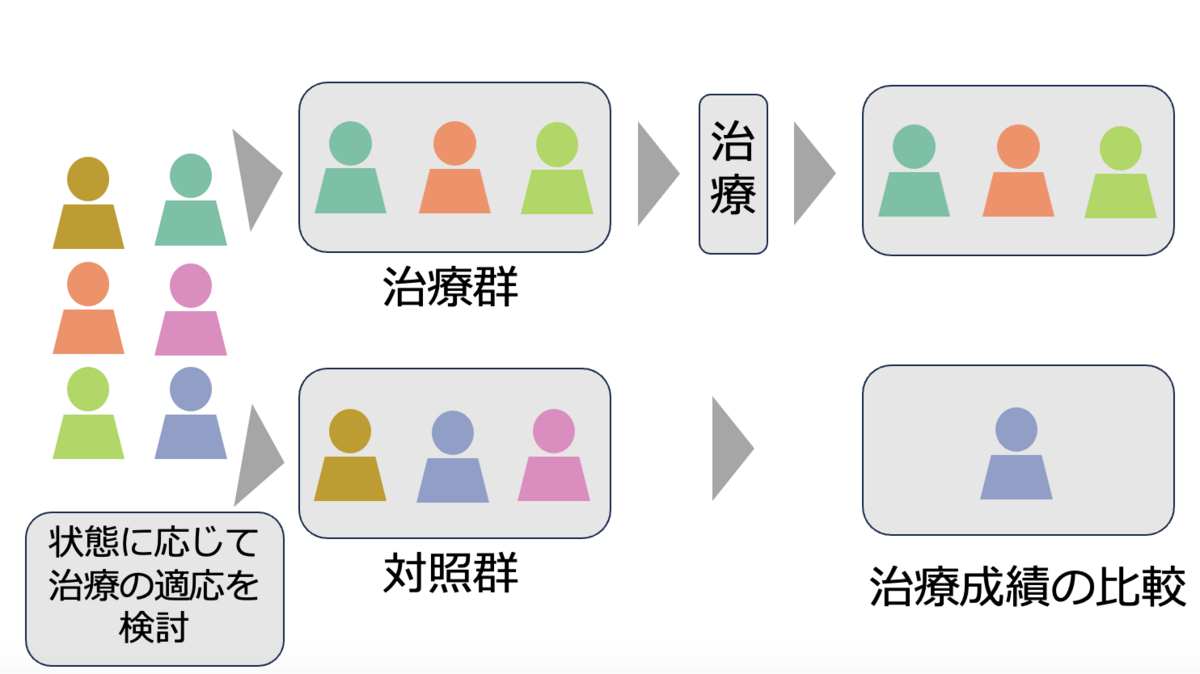
target trial emulationは以下の2ステップで構成されます。
①どのような因果関係が知りたいのかを明確にしてそれを明らかにする仮想RCTをデザインする
第1段階は、どのような因果関係が知りたいのか？を明確にし、それがたとえ非現実的であろうと、RCTの形で定義します。現実的にはRCTが何らかの理由でできないにしろ、その制約がなかったと考えて、（例えば金銭的制約があるのであれば無限のお金があると仮定し、）「仮想RCT」を想定します。 実際に、RCTをやるなら、どのような患者を組み入れるのか、どのような治療を、どのような薬の量、期間で、どのように割り当てを行い、アウトカムをどのように設定し、どのように追跡し、どれくらいの期間追跡するか、どのように解析するかなどをできるだけ詳細に定義します。
②実際に観察データを利用して仮想RCTを模倣する
第2段階は、観察データを使用し「仮想RCT」の手順を模倣します。 上で定義した手順通りにデータベースから適格なデータを見つけ、割り当てを行い、治療を行ったとして、アウトカムが生じる、あるいは実験終了までを追跡し、同じ解析を実施します。しかし、観察研究であり、ランダムな割り付けはできないため、割り当てだけは傾向スコアマッチングなどを利用して擬似的な割り当てを行います。
観察研究ではランダムな割り付けは難しい
傾向スコアマッチングに関してはこちらの過去記事をご参照ください。 syleir.hatenablog.com

仮想RCTにおいて定義すべきもの

適格基準、治療戦略、割り当て手順、追跡期間、アウトカム、効果の種類、分析計画を定義する必要があります。
適格基準
適格基準という言葉はわかりにくいですが、「組入れ基準」＋「除外基準」とざっくり考えるとわかりやすいと思います。 有名なPI(E)COで考えるとP(Population)に該当します。「どのような患者を入れて、どのような患者を除外するか」を定義します。
治療戦略
治療戦略については、PICOでいうI, C(Intervention, Conparison)に相当します。 治療群、対照群を明確に定義していきます。治療群については、どのような介入をいつからいつまで行うのかを決めます。本来のRCTではどのような治療を行うか、を考えます。 これを観察研究で模倣するときは、ビッグデータの中から適格基準を満たし、そのような治療を行った人を抽出し治療群とします。一方で対照群はビッグデータの中から適格基準を満たし、治療を行わなかった人を抽出し対照群とします。
割り当て手順
仮想RCTではランダム化による割り当てを行います。予見不可能な割当てを行う必要があります。治験責任医師や関与する医療関係者が（デザイン上可能であれば）その割り当てを知ることがないように行います。しかし、観察研究ではランダム化が難しいので、傾向スコアマッチングなどで患者背景の調整を行います。（上で書いた通りです。）
追跡期間
次に、追跡期間を定義します。開始時間と終了時間を決めます。 仮想RCTでは追跡期間の開始時間はランダム化時点（参加登録時点）です。 終了時間はアウトカムが起こった時、または観察終了時点までが一般的だと思います。 これを観察研究で模倣するときが一癖あり、追跡終了時点の決定は比較的容易で、仮想RCTと同様にアウトカムが起こった時、あるいは追跡開始時点から一定時間経過した時で良いと思いますが、追跡開始時点（time zero）については、きちんと決めないといけません。ここを曖昧にしてしまうとimmortal time bias(不死時間バイアス)などのバイアスが生まれる原因になってしまいます。バイアスの説明はここで書くと相当な分量になってしまうので、またいつか書きます。 一般的なのは適格基準を（初めて）満たしたときとすることですが、これは治療が割り当てされる前に確実に適格基準を満たすように定義しなければなりません。過不足なく、確実に明確になるように適格基準を決める必要があります。
アウトカムの設定
RCTにおけるアウトカムの重要性についてはもはや言うまでもないでしょう。RCTは研究テーマに対する科学的根拠に基づいた答えを導き出すようにデザインされるべきで、そのテーマに関連するアウトカムを設定する必要があります。またそのアウトカムは測定できることが必要です。 観察研究についてもRCTで検討されるべきアウトカムと同様のものを設定します。
効果の種類
ITT(intention to treat)効果、PP(per-protocol)効果のどちらを設定するかどうかを決めます。 ITTは当初の治療戦略を継続するかにかかわらず、当初の治療戦略としたかどうかの比較であり、治療選択の逸脱自体 も治療効果と考えます。 PPは逸脱があった場合は打ち切りとして扱います。時間依存性曝露を扱う必要があるので、IPTW（逆確率重み付け法）などで扱う必要があります。
分析計画
仮想RCTではどのように解析するかや使用する統計モデルを事前に決定しておく必要があります。 事後解析する場合はそれを明記する必要があります。 観察研究として模倣する場合も事前にどのような解析を行うかは決定しておく必要があります。

target trial emulationの限界

さて、ここまで説明したところですが、target trial emulationはあくまで「考え方」ということが理解できたでしょうか。 道具だけ揃えても職人になれないように、Ude⚪︎yの講座だけ買ってもデータサイエンティストになれないように、#駆け出しエンジニアと繋がりたいのハッシュタグを使ってもエンジニアにはなれないように、target trial emulationだけあっても上手に因果推論ができるわけではありません。良い研究はいいCQやRQから生え、適切なデータベース構築をし、因果推論手法を理解して使わないといけません。 ただ、観察研究のやり方を提示し、大枠を示してくれたという意味では大いに有意義なフレームワークです。より良いものを真似する、シンプルでありながら大変有効なのでぜひ使ってみてください。

おわりに

この記事を書いている途中で
医学研究のための　因果推論レクチャー

医学研究のための　因果推論レクチャー

Amazon
これが発売されました。この中にもtarget trial emulationについても軽く触れられており、知っている限り初めての邦書だと思います(違ったらスミマセン、教えてください) 因果推論について初歩から学べる本で薄いのに充実している印象を受けました。ぜひ。

カプランマイヤー曲線の作成（打ち切りのある場合）【Part5】【統計検定1級、凖1級対策】

1. はじめに

前回の記事はこちらです。
syleir.hatenablog.com

前回は、打ち切りのない場合でカプランマイヤー曲線を作成してみました。
今回は、打ち切りのある場合でも生存曲線をカプランマイヤー法で作成できるようになるべく、解説していきます。

本稿では

エモリー大学クラインバウム教授の生存時間解析

エモリー大学クラインバウム教授の生存時間解析

Amazon
Survival Analysis: A Self-Learning Text, Third Edition (Statistics for Biology and Health)

Survival Analysis: A Self-Learning Text, Third Edition (Statistics for Biology and Health)

Amazon

これらの本から統計検定対策として必要十分なように要約、加筆しています。
わからないところがあれば原著にあたってみてください。

2. 目次

3. 打ち切りのある場合

適宜、前パートと対応しているので、2タブで開きながら見てみてください。

3.1 打ち切りとは

前回述べたように、打ち切りデータは、観察期間外にイベントが起きていることを指します。最もこの中で多い例は、観察期間が終了した時点でイベントが発生していない、という例であり、「右側打ち切り」という概念に含まれます。現状試験対策では右側、左側などの理解は不要ですが、重要な概念なのでいずれ補足記事を書きます。

「観察期間が終了した時点でイベントが発生していない」というのは、例えば、治験などで、死亡をイベントとしたときに、「観察期間が終了した時点で被験者がまだ生存している」といった状況を指します。イベントが起きる前に実験期間が終了してしまうケースは非常によくあることです。
打ち切りのないデータを得るには患者全員が亡くなるのを待つ必要がありますが、到底（経済的や時間的制約により）現実的ではありません。

3.2 打ち切りのあるデータの取り扱い

理想的には、打ち切りのないデータを集めるのが理想ですが、多くの実験の場合、それが難しいことは想像に難くありません。
ではどのように対応したら良いでしょうか。
例えば、打ち切りが発生したデータをそもそもそのような人がいなかったこととして、データが無かったことにした場合どのような問題があるでしょうか。
この場合は、「少なくとも打ち切られるまではイベントが起きることなく推移した」という情報を失うので、イベントの発生率やハザードを過大評価してしまいます。特に打ち切りが多ければ多いほどそのようになってしまい、解析に必然的に打ち切りが絡む生存時間解析では無視することはできない影響を与えてしまいます。

そこで、打ち切りを含むデータは生存時間解析において特別な扱いが必要で、これを考慮に入れた生存関数の推定を可能にするのがカプランマイヤー推定量であり、それに引き続くカプランマイヤー法です。

3.3 カプランマイヤー推定量とは？

まずは定義を出します。

\hat{S}(t_{(f)}) = S(t_{(f-1)}) \times (1 - \dfrac{n_f}{r_f})

ここで、
r_fは時間t_{(f)}の直前まで生存している人数
n_fは時間t_{(f)}でのイベント（例えば死亡）数
を表しています。

さて、この式はすでに既出です。1章の最後と比較して全く同じ式です。そう、カプランマイヤー統計量とは、生存関数の推定値を出すための補正を行ったものなのでした。

カプランマイヤー統計量の更新は上と同じようにイベントが発生するごとに情報を更新していきます。伏線回収ですね。打ち切りがあっても情報の更新を行わず、イベントが発生した際に情報の更新を行います。

情報の更新の仕方も全く前と同じです。
①' T = tの直前のS(t)の値
②' T = tでのイベントの発生率
を情報として持っておき、①'×②' とすることで生存確率を更新します。
イベントの発生率も同じ計算でよく、その時点での 1 - \dfrac{死亡人数}{直前生存人数}です。

唯一打ち切りのない場合と違うのは、「直前生存人数r_f」にイベント間に発生した打ち切りの影響が含まれることです。このおかげで、前述したイベントの発生率やハザードを過大評価してしまうことを防ぐことができます。なお、補足ですが、この「直前生存人数r_f」のことをリスクセットと言います。

4 練習問題

さて、ここまでの知識を整理するために練習問題として以下のデータを使ってカプランマイヤー曲線を作成してみましょう。

t イベント発生数 打ち切り数 リスクセット
0 0 0 6
1 2 0 6
2 0 0 4
3 0 1 4
4 1 0 3
5 1 0 2
6 0 0 1
t = 0

t = 0では、\hat{S}(0) = 1です。

t = 0
t = 1

\hat{S}(0) = 1であり、t = 1での直前生存人数：リスクセットは6 ,イベント発生数は2なのでt = 1でのイベント発生率は1/3ですから、推定されるt = 1での生存率\hat{S}(1)は1×(1 - 1/3) = 2/3となります。

t = 1
t = 2

t = 2ではイベント、打ち切り共にありませんので、そのまま\hat{S}(2)は2/3のままです。

t = 3

t = 3では打ち切りが1件あります。
イベントはないので生存関数の値の更新はありません。
リスクセットが1減って4 → 3に変わります。

t = 3
t = 4

t = 4ではイベントが1件、リスクセットは3件なので、 t = 4でのイベント発生率は1/3です。
よって推定されるt = 4での生存率\hat{S}(4)は2/3 ×(1 - 1/3) = 4/9となります。

t = 4
t = 5

同様にt = 5ではリスクセット2件、イベント1件なのでイベント発生率は1/2
よってt = 5での\hat{S}(5)は4/9 × (1 - 1/2) = 2/9 となります。

t = 5
t = 6

t = 6ではイベント、打ち切り共にありませんので、そのまま\hat{S}(6)は2/9のままです。

完成
完成！

ということで完成になります。

実際はステップ関数の形で表しますのでこれを折れ線のように表して

このようになります。

なお、過去問の解答ではそういう表記はないのですが、一般的には打ち切りがある場合は上髭をつけて表記することが多く、

このように表記します。

おわりに

今回は打ち切りのある場合についてもカプランマイヤー曲線の作成ができるようになりました。
次回は、実際の解析を行うためのログランク検定について解説をします。

カプランマイヤー曲線の作成（打ち切りのない場合）【Part4】【統計検定1級、凖1級対策】

1. はじめに

前回の記事はこちらです。
syleir.hatenablog.com
前回は、生存関数、ハザード関数とは何か、どのように計算するのかをいくつかの例題を交えながら説明したのでした。
今回は、カプランマイヤー曲線の作成に主眼を置きながら解説していきたいと思います。
今回のパートでは打ち切りのない場合でカプランマイヤー曲線の作成ができるようになることが目標です。
なお、打ち切りについては次回説明しますが、打ち切りによって不完全な情報のデータが生まれるという理解をしてください。
つまり、今回は完全なデータでカプランマイヤー曲線を作ることが目標です。

本稿では

エモリー大学クラインバウム教授の生存時間解析

エモリー大学クラインバウム教授の生存時間解析

Amazon
Survival Analysis: A Self-Learning Text, Third Edition (Statistics for Biology and Health)

Survival Analysis: A Self-Learning Text, Third Edition (Statistics for Biology and Health)

Amazon

これらの本から統計検定対策として必要十分なように要約、加筆しています。
わからないところがあれば原著にあたってみてください。

2. 目次

3. 生存時間解析の目的

そもそもカプランマイヤー曲線は生存時間解析の一分野です。Part2でも述べたように、生存時間解析の主眼は、どれくらいの時間が経過した状態で、どれだけの人が生存しているかという生存数-時間関係の解析でした。
そこで生存関数S(t)を導入し、生存関数S(t)は時刻tを超えて生存する確率を見ることで、時間と生存数の関係性を視覚的に理解することが可能になります。

4. カプランマイヤー曲線とは

誤解を招くことを承知で簡易化すると、実際のデータから作った生存曲線のことです。

通常、モデリングで使用する生存関数は例えば前のPartで説明したようにy = exp(-x)のように「綺麗な」関数を用いることが多いです。

生存関数の一例


しかし、実際の解析では実際のデータから生存関数を推定したいというモチベーションが強いです。
その際に最もよく使われるのが「カプランマイヤー推定量」を用いて生存曲線を作成する「カプランマイヤー法」であり、これにより作られた生存曲線が「カプランマイヤー曲線」です。
用語が複雑ですが、ここはそんなもんという雑な理解で大丈夫です。追って説明します。
離散的な実際のデータから推定される曲線は、通常ステップ関数の形を取ります。

実際のデータから推定される生存曲線の例

生存時間解析において、観察期間外にイベントが起きていることを打ち切りと言います。厳密にはもう少し勉強するべきことがありますが、これを話すと1章必要なのでいずれ番外編で書きます。
打ち切りが起きたデータは生存時間解析において特別な扱いが必要となります。
カプランマイヤー法はこの打ち切りデータを考慮に入れた生存関数の推定を可能にします。

5. 打ち切りのない場合

簡単のためにまず、打ち切りがない場合を考えます。

t イベント発生数 生存数 生存率
0 0 5 1
1 2 3 0.6
2 0 3 0.6
3 0 3 0.6
4 1 2 0.4
5 1 1 0.2
6 0 1 0.2

非常に簡単な例ですが、これの生存関数を推定しようと思った場合、生存率を点推定値としてグラフを書いてみたらよいという、自然な発想があります。このようになります。

とりあえずプロットしてみる

ところで、知りたいのは生存"関数"である以上、離散的でなく、連続的に定義されてほしい性質があります。イベントが起きていない間の推定はどうしたら良いでしょうか。

ここは、色んな推定の考えがあって良いところだと思います。
・点と点を直線で結び、折れ線にする
・最小2乗法のように曲線をフィッティングする
など、案としてはありうると思いますが、今回は説明の便宜上、その点から次のイベントが起きるまで右に伸ばして補完することにします。
また、t = 1 などの境界域では実際のイベントを反映した後の値を反映することにします。つまり上のグラフのプロットの値を優先することにします。（t=1 でS(t) = 0.6とする）

t >= 0 で定義されるように拡張する

さて、通常このグラフを作る時はどのような思考法をするでしょうか。一般的には例えば、t = 5ではt = 5での生存数が1、元々の生存数が5なのでS(5) = 1/5 = 0.2とするのではないでしょうか。

つまり、情報としては
①元々の生存数
②T＝tでの生存数
を持っていることが多いと思います。しかし、発想を変えて**情報の持ち方を変える**ことで打ち切りのあるデータにも対応できるようになります。

その持ち方とは
①' T = tの直前のS(t)の値
②' T = tでのイベントの発生率
です。

この例では、①' : t ＝ 5の直前のS(4.999…)＝0.4 と②' : t = 5でのイベント発生率1/2 = 0.5を情報として持ち、S(5) = S(4.999...) × 0.5 = 0.2として情報を更新していきます。

具体的にはこの図のようにイベントが発生するごとに情報を更新していきます。この、イベントが発生するごとに更新していくという考え方は非常に重要で今後も出現するので覚えておいてください。

グラフの作り方を工夫する

より厳密には、イベントが発生した時刻をt_{(1)}, t_{(2)}, …, t_{(f)}, …
と並べると、

時間 t_{(f-1)}から時間 t_{(f)}まではイベントが起きないので、
（時間t_{f}まで生き残る確率）＝（時間 t_{(f-1)} まで生き残る確率）✖️（次に時間 t_{(f-1)} まで生き残った下で、時間t_{(f-1)}を超えて生きる確率）
となり、生存確率は「それまでの生存確率」と「その時点での生き残り確率」の積で計算できるということです。
それまでの生存確率は帰納的に同様に計算できますから、「その時点での生き残り確率」が重要になると考えられます。データに打ち切りがない場合には、「その時点での生き残り確率」は次のようにして推定ができます。

（t_{(f)}での生き残り確率）
＝Pr[T > t_{(f)}
＝T = t_{(f)}でイベントが起こらない確率
＝ 1 - \dfrac{n_f}{r_f}

ただし
n_f : t_{(f)}で発生したイベント数
r_f : t_{(f)}直前での生存症例数です。

よって、生存関数の推定が、
「生存確率」＝「それまでの生存確率」×「その時点での生き残り確率」でできることから、
S(t_{(f)}) = S(t_{(f-1)}) \times (1 - \dfrac{n_f}{r_f})
と表すことができます。

おわりに

このパートでは、打ち切りのない場合の生存関数の推定を行いました。「それまでの生存確率」、「その時点での生き残り確率」として情報を持つことが重要なのでした。
次回は、打ち切りのある場合にどのように考えたら良いかを解説します。

次回記事です。
syleir.hatenablog.com

【Part3】統計検定準1級•1級 生存時間解析のまとめ【生存関数・ハザード関数】

はじめに

更新が大変滞っており2ヶ月ぶりの更新です。申し訳ありません。

前回の記事です。
syleir.hatenablog.com

基本的な考え方について解説しました。

このパートでは生存時間解析において数理的な解析をする時に重要な概念である生存関数、ハザード関数について整理しておきます。
生存関数、ハザード関数の理解なくして生存時間解析の理解はありません。大変ですが、内容は高校数学程度なので頑張りましょう。

前提知識の確認

すでに十分な理解がある方は適宜飛ばしてください。

生存関数

生存関数はある時刻において生存している確率に主眼を置いています。

確率密度関数f(t)があり、tが時間を表しているとき、その確率変数TがT>tを満たす確率のtに対する分布を確率密度関数としてS(x)と表したものです。つまり、生存関数S(t)は時刻tを超えて生存する確率、つまり、確率変数Tが特定の時間tを超える確率を表しています。

定義としては

S(x)= P(X > x) = \int_{x} ^ \infty f(t) dt

です。

性質としては、
S(x) = \int_{x} ^ \infty f(t) dt = P(X>x)= 1 - P(X \leq x)= 1 - \int_{-\infty} ^x f(t) dt = 1 - F(x)
が成立します。

ハザード関数

ハザード関数h(x)は被験者が時刻xまで生存したもとでのその瞬間の死亡の多さを定量的に表したものです。注意すべきなのは確率ではないため、1を超えることもあります。

定義は、
h(x) = \lim_{\Delta x \rightarrow 0} \dfrac{P(x \leq X \leq x + \Delta x | X \geq x)}{ \Delta x}

です。つまり、h(x) \Delta x がxからx+\Delta xまでの間の死亡確率を表しています。

ここで、極限の中身の分子を上の条件付き確率の定義に従って式変形すると、
P(x \leq X \leq x + \Delta x | X \geq x)
= \dfrac{P(x \leq X \leq x + \Delta x \cap X \geq x)}{P(X \geq x)}
= \dfrac{P(x \leq X \leq x + \Delta x)}{P(X \geq x)}

です。2行目から3行目の式変形については、数直線を書けば（書かなくても）自明ですが、
x \leq X \leq x + \Delta xという条件は X \geq xを完全に包含していますから、
P(x \leq X \leq x + \Delta x \cap X \geq x) = P(x \leq X \leq x + \Delta x)なので成り立ちます。

以下Xが連続であれば、この変形を利用すれば、
h(x) = \lim_{\Delta x \rightarrow 0} \dfrac{P(x \leq X \leq x + \Delta x | X \geq x)}{ \Delta x}
= \lim_{\Delta x \rightarrow 0} \dfrac{P(x \leq X \leq x + \Delta x)}{P(X \geq x) \Delta x}
= \lim_{\Delta x \rightarrow 0} \dfrac{F(x + \Delta x) - F(x)}{\Delta x} \dfrac{1}{S(x)}
= \dfrac{f(x)}{S(x)}

となります（微分の定義）。この式から、h(x)はS(x)から導くことができます。

また、累積分布関数F(x)はF(x) = P(X \leq x) = 1 - P(X > x) = 1 - S(x)となるので、両辺微分して
f(x) = -S'(x)
を利用すると

h(x) = \dfrac{S'(x)}{S(x)} ＝ - \dfrac{d}{dx} log(S(x))

したがって、h(x)の累積ハザード関数としてH(x) = \int _0 ^ x h(x) = - log S(x)を定義すれば、S(x)からH(x)を計算でき、それを微分することでh(x)が計算できることになります。

これで、h(x)とS(x)が相互変換可能であることがわかりました。
当然、h(x)とS(x)からはf(x)も計算できます。

練習問題

h(x)とS(x)、f(x)が相互変換可能であることを利用していくつか計算問題をやってみましょう。

例題1

h(x) = 1 の時、S(x), f(x)は？
H(x) = x = - log S(x)なので　S(x) = exp(-x)

f(x) = -S'(x) = exp(-x)

例題2

h(x) = \lambda の時、S(x), f(x)は？(指数分布)

H(x) = \lambda x = - log S(x)なので S(x) = exp(-\lambda x)

f(x) = -S'(x) = \lambda exp(-\lambda x)

例題3

f(x) = \dfrac{\theta \lambda^\theta}{x ^ {\theta + 1} } (\theta > 0, \lambda > 0, x \geq \lambda)の時、h(x), S(x)は？（パレート分布）
S(x) ＝ \int _ x ^ \infty f(x) = \int _ x ^ \infty \dfrac{\theta \lambda^\theta}{t ^ {\theta + 1} } dt
= -[ \dfrac{ \lambda^\theta}{t ^ {\theta} }]^\infty _ x=\dfrac{ \lambda^\theta}{x ^ {\theta} }
H(x) = - logS(x) = \theta log (x) - \theta log(\lambda)
h(x) = \dfrac{d}{dx}H(x) = \dfrac{\theta}{x}

または

h(x) = \dfrac{f(x)}{1-F(x)} = \dfrac{f(x)}{S(x)} = \dfrac{\theta \lambda^\theta}{x ^ {\theta + 1} } \dfrac{x ^ {\theta} }{ \lambda^\theta}= \dfrac{\theta}{x}

例題4

S(x) = exp(-\lambda x ^ \alpha)(\alpha, \lambda > 0, x \geq 0) の時、f(x), h(x)は？(ワイブル分布)

f(x) = - \dfrac{d}{dx} S(x) = - \dfrac{d}{dx} exp(-\lambda x ^ \alpha) =\alpha \lambda x ^ { \alpha - 1} exp(-\lambda x ^ \alpha)
h(x) = \dfrac{f(x)}{S(x)} = \dfrac{\alpha \lambda x ^ { \alpha - 1} exp(-\lambda x ^ \alpha)}{exp(-\lambda x ^ \alpha)} = \alpha \lambda x ^ { \alpha - 1}


以上を通じて、相互変換可能性というものがお伝えできたでしょうか。

かなり恣意的な関数が例題に上がっていますが、積分不可能であったりする関数も世の中には多いためです。そういう時はコンピュータシュミレーションで頑張りましょう。

ハザード関数の意義

では、相互変換可能なのであれば、どうしてハザード関数を用いるのでしょうか？
もともとの確率密度関数f(x)や、生存関数S(x)を使った方がわかりやすいのではないでしょうか？
本章ではハザード関数がなぜ存在するかを説明していきます。

視覚化としての意義

もちろん生存関数をグラフ化してもどこでたくさんイベントが起こっているかはわかりますが、ハザード関数として描出した方が、時間あたりのイベントの起こりやすさが可視化しやすいです。生存関数を見せられるよりは、イベントがどのタイミングで起こりやすいのかを見せた方が、人間は理解しやすいです。

モデリングとしての意義

さらに、ハザード関数は予測モデルの作成にも使用されます。なぜ可視化するのかの大きな理由が、「直感的に理解しやすいから」です。人間が理解できる関数を使うことで、実世界の事象を記述しやすくなります。

ハザード関数を使用する方が、簡単にモデリングができ、直感的にわかりやすいです。ハザード関数を用いたモデリングの例がCox比例ハザードモデルで、疾患のリスク要因や治療効果を評価するのによく用いられます。統計検定の出題範囲にも含まれています。それはおいおい扱いたいと思います。

おわりに

少しヘビーになってしまいました。凖1級の勉強としてはここまで、あるいはこの次までで良いと思います。
次回以降は具体的な応用、カプランマイヤー曲線について話したいと思います。

次回記事です。
syleir.hatenablog.com

【Part2】統計検定準1級•1級 生存時間解析のまとめ【導入・考え方】

はじめに

前回の記事では過去問の分析、現在の勉強方法などについて書きました。今回は生存時間分析の「お気持ち」、普通の解析と何が違うのか、何をしたくてこんなことをするのかについてまとめていきたいと思います。
何が見たいかがわかると、なんでこんな式が登場するのかの理解がとてもやりやすくなります。
ちなみに、ワークブックの行間を埋めることを目標としているので、こういう「お気持ち」の解説に一番力を入れています(笑)

目次

生存時間解析とは？

生存時間解析というと、その名称から「死亡までの時間」についての解析だというイメージがつきまといますが、実際にはそれに限らず、もっと幅広い分野で使われている解析です。生存時間データ解析とは、「イベント」までの時間データに対する解析という意味です。「イベント」は、「死亡」でなくとも良いのですが、生存時間解析ではよく死亡を扱うため、生存時間解析と呼ばれています。よって、取り扱われるテーマとしては、次のようなものがあり、多岐に渡ります。また、「イベント」はネガティブなものだけでなく、ポジティブなものでも構いません。

・疾病の再発までの時間
・疾病の治癒までの時間
・工業製品が故障するまでの時間
・マッチングアプリのカップル成立までの時間
・もちろん統計検定の合格までの時間などもテーマとしては悪くないでしょう。

ただ、やはり主要な目的としては、どれくらいの時間が経過した状態で、どれだけの人が生存しているかという生存数-時間関係の解析です。
これを省略して生存(数-)時間(関係の)解析と思っていただくのが1番スマートかと思います。

通常の回帰分析との違い

ところで、通常の回帰分析でも死亡をアウトカムにした分析ができると思いませんか？ここをはっきりさせることが、生存時間分析の文脈においては非常に重要です。回帰分析と生存時間解析の違いが、直接そのまま生存時間解析の特徴であり、勉強しなければいけないことになります。

1.なにに関心を置いているか

通常の(重)回帰分析で死亡の解析をする時のモデリングは
y = \beta_0 + \beta_1 x_1 + ... + \beta_n x_n + \epsilon
などとして計算します。この yに死亡しているかどうかを入れ、 \betaに興味関心のある共変量を入れて解析します。
つまり、回帰分析で知りたいのはアウトカム-共変量関係です。平たくいうと、「何が死亡に影響を与えているか」を関心にしています。5W1Hで言うとWhatに関心があります。共変量に時間を表す要素を入れない限りは、時間依存的な解析は起きず、アウトカムを取った時間でのみの解析をしていることになり、途中の時間で何が起きているかはそもそもデータを取っていないため解析できません。
全然厳密ではないですが、イメージはこうです。

通常の回帰分析では時間経過に関心が(あまり)ない

ちなみに脱線しますが、共変量に時間を入れた回帰分析はあります。興味があれば読んでみてください。
【統計的因果推論】分割時系列解析の初歩を解説する【ITS 回帰不連続デザイン】 - Syleir’s note

一方で、生存時間解析で興味があるのが、先ほど述べたように生存数-時間関係です。5W1Hで言うとWhenに関心があります。共変量をモデルに組み込むこともできますが、主眼としては、その結果、どのタイミングでイベントが起きやすいかに関心が主にあります。
つまり、生存率ー時間関係が時間経過でどのような経過を示すのか、に興味関心が強いと言うことになります。
どのような経過を示すのか、を説明するものが、「ハザード比」や「生存関数」といったもので、これらを学ぶ必要があります。

生存時間解析では生存率ー時間関係を丁寧に観察する

2.データの性質

1.で述べたこととも関連がありますが、生存時間解析ではデータの取り方も時間ごとに丁寧にデータを取ります。通常の回帰分析ではアウトカムの評価をするタイミングでデータを取るのに対し、生存時間解析では解析対象によって、年、月、週など時間軸は異なりますが、時間ごとにデータを取る必要があります。また副作用などで離脱した人（打ち切り：後で説明します）のデータも細かく収集します。

3. 統計モデル

通常の回帰分析では、線形回帰、ロジスティック回帰などの手法で解析しますが、生存時間解析には特殊な解析手法を用い、生存時間解析には、生存曲線を推定するためのKaplan-Meier法やハザード比を評価するためのCox比例ハザードモデルなど、イベントのタイミングにフォーカスを当てた専用の統計モデルがあります。

まとめると、生存時間解析は時間に関する情報を重視し、イベントが発生するまでの時間に焦点を当てるのに対し、通常の回帰分析は時間をあまり気にせず、イベントの発生を予測することを目的とします。時間に依存する状態を知るため、「ハザード比」、「生存関数」、「データの取り方」、「打ち切り」、「Kaplan-Meier法」、「Cox比例ハザードモデル」など生存時間解析に特異的な学習をする必要があります。

そしてこれは、前記事の到達目標で述べた
・生存関数などの数式的な定義を理解し、初歩の考え方を学ぶこと、それにより各関数が計算できるようになっていること
・カプランマイヤー曲線の作成、ログランク検定、ハザード比の推定、そして比例ハザードモデルの理解
で概ね達成できていることが分かります。

おわりに

次回以降の記事で学習内容について1つずつ解説をしていこうと思います。遅筆ですがお待ちいただけますと幸いです。

【Part1】統計検定準1級•1級 生存時間解析のまとめ【過去問の分析・出題内容・勉強法】

はじめに

統計検定準1級のメインテーマと言えるかはわかりませんが（そもそも範囲が膨大すぎてメインテーマなんてないのかもしれません）、今日は生存時間分析について扱っていきたいと思います。
統計検定準1級のバイブルといえば

日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック

日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック

  • 学術図書出版社
Amazon
ワークブックですが、なぜか生存時間分析だけ謎の亜空間に閉じ込められています(第2章、確率分布の中に記載があります)。確かに出題頻度としては低いのですが、なんとか救い出して体系的に整理したいと思ってこの記事群を作成します。

また、1級では統計応用、医薬生物学のメインテーマになります。
今回は凖1級としては十分レベル、1級を6割程度カバーするレベルまでの生存時間解析の初歩を、試験対策という観点からまとめていきたいと思っています。

目次

敵を知る

科目としての性質

生存時間解析は統計検定2級に登場しない新概念で、新しく勉強することが必要になります。言葉の定義、数式の意味、なぜこのようなものを定義するのかを大事にすることが効率の良い学習に繋がった体験があり、一方で高校数学程度の確率、微積分の知識があれば、統計検定準1級くらいの問題は難なくクリアすることができます。

出題範囲表

さて、ありとあらゆる試験対策をするとき、どのような位置付けでその範囲が出題されているのかを常に考慮する必要があります。

引用：統計検定Hp
驚くべきことに、統計検定準1級における出題範囲の定義としては確率分布と母関数のコーナーに細々と存在しているだけなのです。
ということで、ワークブック上もこれに則って確率分布の一種としての紹介にとどまるわけです。
体系的に整理する必要がないのもわかりますね。

ついでに1級の出題範囲も見てみましょう。

1級においては統計数理では統計検定準1級と同様に確率分布と母関数のコーナーに位置付けられていること、
統計応用の医薬生物学分野で生存時間と繰り返し測定という分野でまとめられていることがわかります。

過去問での出題状況

さて、過去問での出題状況を確認してみましょう。具体的な出題内容に関しては実際の過去問を参照してください。
2014年 1級 統計応用 医薬生物学 問4
(1)確率密度関数が与えられた状態からの各関数の導出(2) カプランマイヤー曲線の作成(3) 尤度関数(打ち切りあり)

2015年 1級 統計応用 理工学 問2
(1)ハザード関数の導出(2)生存関数の導出 (3)確率密度関数の計算 (4),(5)統計数理的問題

2016年 1級 統計応用 医薬生物学 問3
(1)カプランマイヤー曲線の作成(2)ログランク検定(3)ハザード関数の部分尤度

2016年 準1級 問8
(1)生存関数から確率密度関数の導出 (2) 確率分布、平均、中央値の計算(3)生存時間の中央値の計算

2017年 1級 統計応用 医薬生物学 問1
(1) ハザード関数の導出 (2) 累積ハザード関数の関係式の導出(3)-(5)統計数理範囲の計算問題(6)サンプリング

2018年 1級 統計応用 医薬生物学 (生存時間解析＜統計数理的な問題)問1
(1)尤度関数(打ち切りなし) (2)尤度関数(打ち切りあり)(3)最尤推定量、フィッシャー情報量(4)デルタ法(5)計算

2019年 1級 統計応用 医薬生物学 問1
(1)カプランマイヤー曲線作成(2)Nelson-Aalen推定量の性質(3)境界内平均生存時間に関する問題(4)生存時間の分散(5)ハザードの最尤推定

2021年 1級統計応用 医薬生物学 問1
(1)ハザード関数の定義式から生存関数、確率密度関数の導出(2)カプランマイヤー曲線の作成(3)競合リスクの処理(4) 表の穴埋め(5)競合リスクの解釈

2022年 1級統計応用 医薬生物学 問1
(1)比例ハザード性(2)比例ハザードモデル(3)比例ハザードモデル下での性質(4)ハザード比の推定

といった感じです。ほぼ毎年何かしらで出題されています。
　

統計検定受験の到達目標

これらを踏まえて、
準1級の対策としては、生存時間解析は過去に1問しか出題はありませんので、生存関数などの数式的な定義を理解し、初歩の考え方を学ぶこと、それにより各関数が計算できるようになっていることで十分であり、
1級の対策としては、凖1級で求められているような、統計数理的な計算をするのはもちろん、カプランマイヤー曲線の作成、ログランク検定、ハザード比の推定、そして比例ハザードモデルの理解までが求められていることがわかります。
これは出題範囲として取り上げられているように、凖1級では確率分布と母関数の中にあり、計算を重視していること、1級では大分野となっており、生存時間解析そのものを理解してくださいというメッセージと私は理解しています。

公式本での取り扱い

準1級対策としては、ワークブックには例題を含めて問題の記載はありません。解説としても紙面5行で終了しています。1級対策としても公式本ではちょっとした解説はあるものの、数ページ程度の解説であり、なかなかこれで理解するのが難しいと思います。最近でた増訂版でも追加はありません。これが、統計検定における生存時間解析の理解を困難にしている要因です。

生存時間解析の勉強法は？

といったところで、今まで生存時間解析を試験勉強として勉強しようと思うと、生存時間解析の成書を読むしかないのでした。
よく使われているのは、

エモリー大学クラインバウム教授の生存時間解析

エモリー大学クラインバウム教授の生存時間解析

Amazon
生存時間解析入門 原書第2版

生存時間解析入門 原書第2版

Amazon
だと思います。前者は解説が冗長なのと、実装に重きを置いているので試験対策としては自分で情報を取捨選択する必要があります。（しかしわかりやすいです。おすすめです。）
後者は難易度がかなり高く、必要とされるレベルを大きく超えます。まだ自分も読み切れていないです。

Survival Analysis: Techniques For Censored And Truncated Data (Statistics for Biology and Health)

Survival Analysis: Techniques For Censored And Truncated Data (Statistics for Biology and Health)

Amazon
個人的におすすめなのはこれですが、英語での出版しかなく、まだ和訳が出ていないです。しかし内容はかなり求められているものに近いと思います。

本記事の目標

ということを踏まえて、生存時間解析という、比較的求められていることがわかりやすい分野で、しかし対策がなかなか難しい、成書を1冊読むのはしんどいという方々へ向けた解説記事を書いていこうと思います。
シリーズを通して、凖1級レベルであれば前半までを読めばわかるように、全て読めば1級問題の前半までは解けるように書いていこうと思っています。
実際の実装はしないので、統計検定受けるつもりはないけど、概念を理解したい、という方にもおすすめです。亀のような更新頻度が想定されますが、よろしくお願いします。

次の記事

coming (as) soon (as possible)...

統計検定準1級対策記事集

はじめに

本ブログの中で統計検定に関する記事をまとめてみました。結構書いているつもりですがあんまり多くなかったです。もっと充実させられるように頑張ります。

受験体験記

2021年度実地試験の体験記です。

syleir.hatenablog.com

使用した教科書・勉強法

各分野別にまとめています。

syleir.hatenablog.com

分野別解説

時系列解析

【Part1】統計検定準1級 時系列解析のまとめ【過去問の分析・出題内容・勉強法】

【Part2】統計検定準1級 時系列解析のまとめ【自己相関係数・定常性】

【Part3】統計検定準1級 時系列解析のまとめ【統計モデリング・ホワイトノイズ】

【Part4】統計検定準1級：時系列解析のまとめ【AR過程】

【Part5】統計検定準1級：時系列解析のまとめ【MA過程】

【Part6】統計検定準1級：時系列解析のまとめ【スペクトル密度関数・スペクトラム】

【Part7】統計検定準1級：時系列解析のまとめ【ダービン・ワトソン比】 

生存時間解析

【Part1】統計検定準1級•1級 生存時間解析のまとめ【過去問の分析・出題内容・勉強法】

ベイズ統計

【統計検定準1級】ベイズ統計学を勉強するための教科書について触れる 

マルコフ連鎖モンテカルロ法（MCMC）

【統計検定準1級】MCMCの初歩のお気持ちをできるだけわかりやすく解説する

ノンパラメトリック法

スピアマンの順位相関係数の導出

 

準1級受験を見据えた2級勉強法

syleir.hatenablog.com

準1級対策になる1級の過去問

syleir.hatenablog.com