1. はじめに
たまには統計検定に関係ない統計記事を書きたいなと思って筆(キーボードでは?)を取りました。需要が迷子ですが、今後HOTになってくると思っているのでよければぜひ。このシリーズは統計的因果推論の文脈で成り立っているので初心者の方はこの記事をご参照ください。
目次
2. 今分割時系列解析がアツい!

これが今回の記事のモチベーションになります。分割時系列解析を用いた論文数は年々増加傾向にあり、人口に膾炙しつつあります。その割には解説記事が(特に日本語のものは)少ないです。原稿案は2年前くらいからあったんですが、そろそろ解放しても良いかと思ったので書いている次第です。
3. 分割時系列解析をなぜ導入するのか?
統計的因果推論において、介入の評価を行いたいときは一般的にランダム化比較試験:RCTを行いますよね。一般的にはランダム化によってさまざまな恩恵が得られ、介入によってアウトカムが変化しているという因果関係を示すことができます。しかしながら対照群を取れないような以下の研究デザインについてはいかがでしょうか。
・ある時間を境に法改正があった前後での事件件数の比較
・治療に対する推奨が変わった後の治療成績の比較
このような例では、介入(法改正や推奨変更)があった世界と、介入がない世界を用意して比較するという、ランダム化比較試験のようなことができません。現実に起きてしまったことは変えられないからです。You cannot change others or the past.ってよく言いますね。それです。
そのような例ではどうしたら良いでしょうか。一つの案としてはその介入が起きていない世界を頑張って探すということが考えられます。法改正に関しては例えばアメリカの特定の州で行われたとすれば、他の州を対照にとる。推奨変更は特定の病院で行われたのであれば他の病院を対照にとるなどが考えられます。この方法の欠点はなんでしょうか?
それは、母集団の違いによって信頼度が落ちるということです。母集団が違うということは、考慮に入れている変数、あるいは入れていない変数すらも調整可能というランダム化比較試験の利点を完全に消しているということです。ある程度の考察は可能ではあるものの、因果推論に用いることができるほどの信頼度は担保できなくなってしまいます。
そこで導入される概念が分割時系列解析です。
4. 分割時系列解析とは?
ということで導入が遅くなってしまいました。この分野はまだ未発展なので英語でのInterrupted Time Series:ITSに対応する日本語表記が曖昧で表記揺れがあったりします。分割時系列デザインとか回帰不連続デザイン、分割時系列解析、中断時系列解析とかって言われてるものは全部これです。この記事では分割時系列解析と呼びます。なんとか統一して欲しいんですが。


なおGoogle的民主主義では分割時系列デザインの方が検索ヒット数が多いですが反抗することとします。理由はカッコいいからです。ただし、時系列解析とは言っても、時系列解析というよりは普通の回帰分析よりの手法なのでそこを注意すると良いと思います。あまり時系列解析要素は出てきません。
4.1 分割時系列解析の概念
分割時系列解析はあるイベントの前と後に分けて、イベントが起きる前のトレンドが続いていた場合を反事実、イベントが実際に起きたあとのトレンドを事実として下図のようにモデリングします。反事実、事実という言葉がわからない場合は冒頭のリンクの記事に立ち戻ってもらえると気持ちがわかるかと思います。

非常に直感的な概念で反事実と事実のグラフが「離れている」ほど介入(イベント)の効果があることがわかります。「離れている」というものの評価も大まかに2つあるのですが、ここでは省略し後ほど説明します。
5. どう実装するか?
反事実部分のモデリングというのは簡単で、ただの回帰分析です。
イベントが起きる前のデータを用いて単回帰すれば良いです。統計検定2級くらいの知識でしょうか。それを直線を伸ばせば良いだけなので中学2年生くらいでもできてしまうかもしれません。問題は事実部分の実装です。
5.1 折れ線回帰モデル(Segmented regression model)
見た目のままですね。このような例では折れ線回帰モデルを使います。
というモデリングをします。
ただし
は実験開始からの時間(横軸)
は処置前後を表す二値変数(0なら処置前、1なら処置後)
は処置が行われた時間
を表します。
これと実際のデータを用いて回帰分析を行い、を決定します。
5.2 パラメータの解釈
さて、このモデルにおける、はそれぞれ何を表すのでしょうか。数式をいじって検討してみます。絶対値を含む式やこのような折れ線というのは場合分けをするのが鉄板です。
5.2.1 処置前
処置前はですから、モデルの式は
となりますね。これは解釈が簡単なのではないでしょうか。
は
における回帰直線の切片であり、
は処置前の傾きです。
5.2.2 処置後
処置後はですから、モデルの式は
となります。これを変形していきます。
となります。 が処置後の傾きということになります。
5.2.3  :なにを表す?
:なにを表す?
処置前の関数で、としてみます。つまり介入直前の値を計算してみます。
となります。
同様に、処置後の関数でとしてみます。つまり介入直後の値を計算してみます。
となります。この差がとなっていることがわかります。
つまり介入前後のにおける切片の差が
になります。平易に言い換えると「介入によって値がどれだけズレたか?」になります。
5.3 パラメータの意味のまとめ
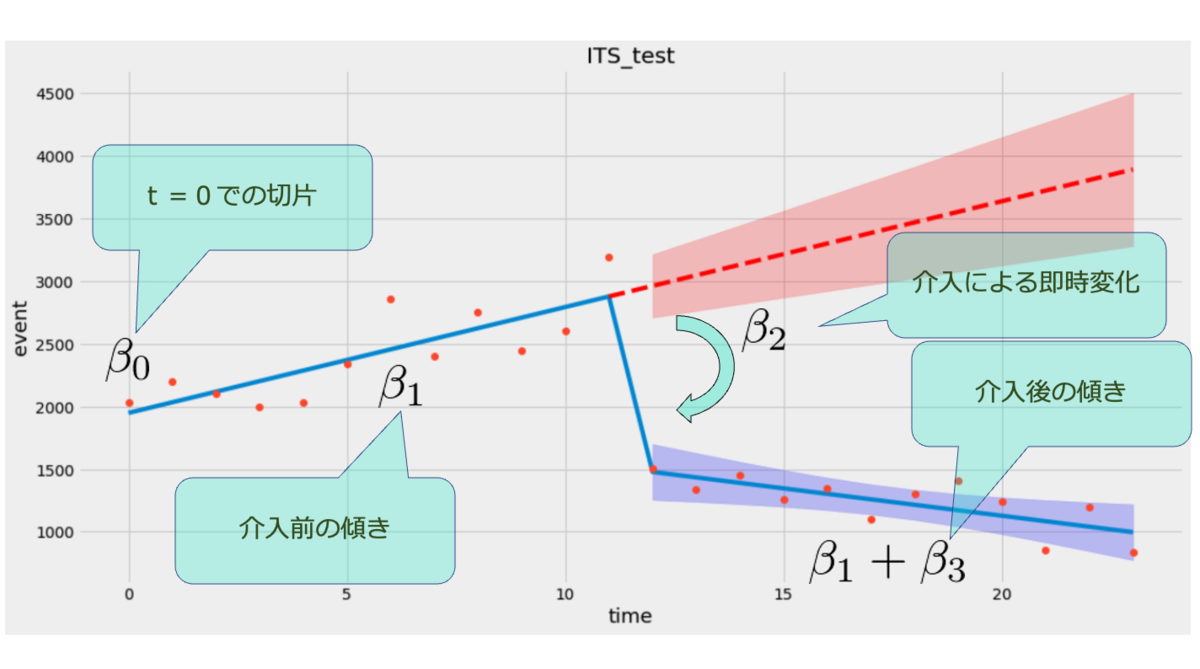
上記をまとめると、
介入前の切片
介入前の傾き
介入前後の切片の差
介入後の傾き
ということになるでしょうか。
これを図解すると下図のようになります。
5.4 level change と slope change
先ほどの章では、反事実と事実のグラフが「離れている」ほど介入(イベント)の効果があると述べました。ここまでをみて、「離れている」の定量評価を考えてみましょう。
介入の効果とは一体なんでしょうか。介入と言えば先日の2022年10月、日銀が為替介入を行いました。自分は為替とかそういうのはサッパリわかりませんが、その結果を見てみましょう。

このチャートからわかるのは
・介入前は上昇トレンドを形成していた。
・介入により即時的な効果はかなり強そう。
・介入後はむしろ介入前より強く上昇している。
ということかなと思います。為替介入が円高方向(グラフの下の方向)に持っていきたい操作であるとすればこの介入は成功なのでしょうか?
少し考えてみると、介入前後でのトレンドの変化とトレンドの即時効果という2点で介入の効果を捉えてみることができそうです。

この図を見てみましょう。
介入前後のトレンドの変化というのは緑の矢印(1本目と3本目)の傾きの変化で表されます。これを、分割時系列解析ではslope changeと言います。slope(スロープ)とは傾きのことです。そのままの意味でわかりやすいですね。この介入では介入したにもかかわらず、上昇の勢いが続いていること、さらに上昇の勢いが強くなっていることがわかります。
続いて、介入の即時的な効果について考えます。
介入の即時的効果というのは青の矢印(2本目)の矢印の大きさで表されます。これを、分割時系列解析ではlevel changeと言います。level(レベル)は水平、水準といった意味です。RPGにおけるレベルは水準から転じて階級と言った意味で使われるでしょうか。ここでいうlevel changeは水平面の変化、水準変化くらいの認識で考えれば良いです。この介入は(この図からはその結論を導くのは尚早ですが)かなりの効果がありそうと見てとれます。
ということで、為替相場については素人ですが、「介入によってかなりの円高に向けた即時効果があるが、その前後では円安への上昇傾向は加速している」というように介入の効果をまとめることができます。
5.5 level change と slope changeの定量評価
さて、これを先ほどのパラメータで考えると、介入前の傾きが、介入後の傾きが
であったので、slope changeは
、介入前後の切片の差が
であったから、level changeは
と表すことができます。極論、分割時系列解析では、
と
を求めるものと言うこともできますね(これは本当に極論ではあるのですが)。
6.まとめ
統計的因果推論の文脈では、ランダム化比較試験などのデザインがよく用いられるが、過去の自分のデータを対照群とする研究デザインもあり、そのひとつが分割時系列解析(ITS)である。ITSにおいては介入前のトレンドが持続するものとして反事実を作り、実際のデータと離れ具合を比較する。その指標がslope change と level change であり、統計的に定量評価が可能になっている。
7. おわりに
長くなってきてしまったので導入はこの辺で終わりにします。次の記事では実際に実装しながら概念の理解を深めていきたいと思います。なお、適用にあたっては細かい前提や実装にあたっての過分散や周期性などの注意点を大きく省略したので各自で勉強されてください。分割時系列解析についてはこの本がおすすめです。
この分野は論文をつまみ食いしながら勉強するしかなかったんですが、やっと最近になって分割時系列解析も成書で扱われるようになってきました。この本は歴史的な背景や論文を挙げながら詳細に解説してくれているのでオススメです。ぜひこの記事を読んで興味が出てきた方は勉強してみてください。Rが読める方はオススメです。読めない方は次の記事を楽しみに待っててください(2週間くらいで頑張ります)。次の記事です。これをPythonで実装しました。
【統計的因果推論】分割時系列解析をPythonで実装する【ITS 回帰不連続デザイン】 - Syleir’s note
