【統計的因果推論】分割時系列解析をPythonで実装する【ITS 回帰不連続デザイン】

はじめに

さて、前々回記事で分割時系列解析、分割時系列デザイン(Interrupted Time Series Analysis : ITS, ITSA)について解説したばかり~~（5ヶ月前）~~ですね。当該記事で2週間後には書くと言った気もしますが。。。
syleir.hatenablog.com
今日はこれをPythonで実装してみたいと思います。

この図を書くのが今日の目標です。
調べてみたところ該当する記事は見当たらなかったので参考にしてください。独力で実装したので改善点、誤りなどあれば教えてください。全実装はページの一番下にあります。目次からもジャンプできます。

はじめに
もくじ
0.使用データ
1.データの読み込み
2.データの前処理
3.変数の抽出
4.モデルの作成と学習
5.学習結果を見る
6.推測を行う
- 別実装
7.反事実データを作成
8.反事実を予測する
9.反事実を描画する
10.信頼区間を表示する
- 信頼区間と予測区間
おわりに
余談
全実装

0.使用データ

date	y
2020-10-01	2030
2020-11-01	2201
2020-12-01	2100
2021-01-01	2000
2021-02-01	2035
2021-03-01	2343
2021-04-01	2854
2021-05-01	2400
2021-06-01	2748
2021-07-01	2443
2021-08-01	2600
2021-09-01	3194
2021-10-01	1506
2021-11-01	1340
2021-12-01	1456
2022-01-01	1256
2022-02-01	1345
2022-03-01	1100
2022-04-01	1304
2022-05-01	1405
2022-06-01	1245
2022-07-01	852
2022-08-01	1200
2022-09-01	840

今回はこのデータを.csvで持ちます。これをpythonで読み込んでデータ処理していきます。~~2022年9月に公開しようと思ってたのでデータは2022年9月までです。~~

1.データの読み込み

import pandas as pd
#ファイルをDataFrameとして読み込む
data = pd.read_csv("dummy_data.csv")

2.データの前処理

読み込んだデータを処理していきます。まずは今回作るモデルの
$Y = \beta_0 + \beta_1 T + \beta_2 X_t + \beta_3(T - T_i) X_t$ を処理していきます。この辺の話は前回記事を参考にしてください。
今回のデータでは2021-10-01に処置開始のイベントが生じたとします。

$T$ は実験開始からの時間
$X_t$ は処置前後を表す二値変数（0なら処置前、1なら処置後）
$T_i$ は処置が行われた時間 $T$ を表します。

import numpy as np

## 研究開始時点から経過した時間T
t = np.arange(0, (len(data)))
data["t"] = t

## 処置前後を表す二値変数Xt
x = np.where(data['date']>="2021-10-01", 1, 0)
data["xt"]=x

### 処置タイミングTiを取得、介入からの経過時間Xt(T-Ti)
ti = data[data['date'] == "2021-10-01"].index
data['xt(t-ti)'] = data['xt']*(data['t']-ti)

ここでdataを出力してみるとこのようになります。

ほしい変数がdataframeに追加されていることがわかります。

3.変数の抽出

説明変数Xから目的変数yを学習するモデルを作ります。余談ですが、慣習的に機械学習分野では(行列は大文字、ベクトルは小文字で表すことに倣って)説明変数は大文字、目的変数は小文字で表します。

#変数の抽出
X = data[['t','xt','xt(t-ti)']]
y = data[['y']]

このように抽出するとXとyは下のようになります。

4.モデルの作成と学習

pythonにおいては回帰分析はscikit-learnなどでもできますが、今回のような詳細なパラメータがほしい場合はstatsmodelsというライブラリを使用します。pythonにおける回帰分析はめちゃくちゃ簡単に実装でき、3行で結果が表示できます。良い時代ですね。add_constantという関数は $y = ax$ ではなく $y = ax + b$ のように定数項も含めて評価してねという関数になります。今回はこれが必要です。

import statsmodels.api as sm

# 回帰モデル作成
mod = sm.OLS(y, sm.add_constant(X))
# 訓練
result = mod.fit() 
# 統計サマリを表示
print(result.summary())

最終行はGoogle ColaboratoryやJupyter notebookのような環境を使っている方であれば単純に

result.summary()

でも良いです。

自分はこちらの方が体裁が整っていて好きです。

5.学習結果を見る

今回の回帰分析で見るのはココです。

ちなみに、この部分を取り出すときはこうです。

coef = np.array(result.params)

としてcoefを出力すると、[ 1948.06410256, 84.41258741, -1483.502331 , -128.06643357]と出てきます。
これは学習結果が、
$Y = \beta_0 + \beta_1 T + \beta_2 X_t + \beta_3(T - T_i) X_t$
において $\beta_0 = 1948, \beta_1 = 84.41, \beta_2 = -1483, \beta_3 = -128.1$ ということを示しています。

6.推測を行う

実際に、この学習した式に対してデータを入れてみたときどのような挙動をするのかを検証してみたいと思います。
これは1行で実装ができて、

#学習したモデルから推測を行う
y_predict = result.fittedvalues

これで終わりです。y_predictを出力してみると

このように出てきます。

ただ、今回はこの式に介入をしていなかったときを想定した反事実の予測もしてみたいので、別実装を用意します。

別実装

#Xの0列目に'cep'というXと同じ長さの[1, 1, 1, ...]という列を挿入
X.insert(0, 'cep', [1]*len(X))

こうすると

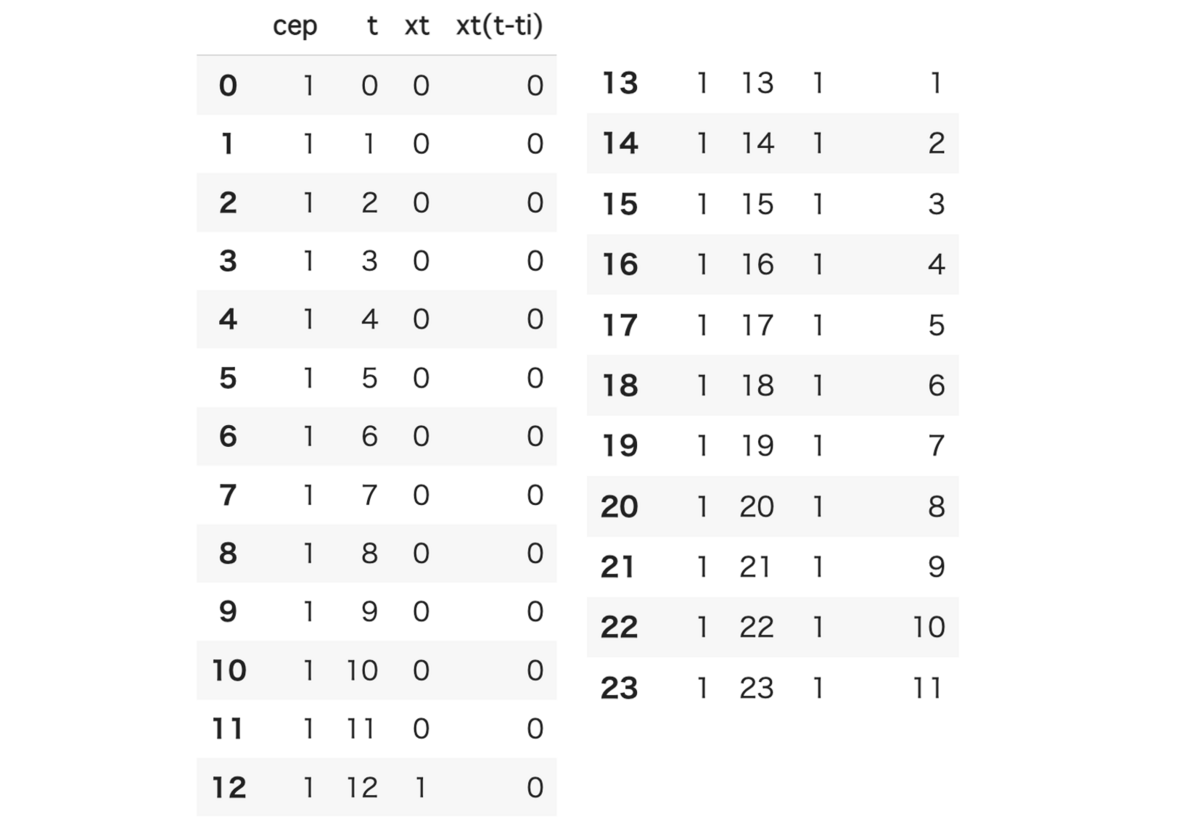
このようにXの0列目に大量の1が挿入されます。この操作は行列のサイズを合わせるために必要で、定数項＝1*定数項とみなしています。
便宜上やるお作法です。

この行列Xを利用して推測をする関数が以下で、実質的には上と変わらない挙動をしていますが、Xを他の行列に置換することで違うXに対しても予測ができます。

#学習したモデルから推測を行う
y_predict = result.predict(X)

この時のy_predictは以下で、上の実装での結果と一致していることがわかります（当然ですが。）

ちょっとここまでの結果を描画してみます。

plt.style.use('fivethirtyeight')

plt.figure(figsize=(16,8))
plt.title('ITS_test')
plt.xlabel('time',fontsize=18)
plt.ylabel('event', fontsize=18)
plt.plot(y, 'o')

plt.plot(y_predict)

まともに学習できていることがわかります。

7.反事実データを作成

さて、統計的因果推論のキモは事実と反事実の違いを描出することでした。
この場合の反事実というのは介入を行っていない、ということに相当します。

元の変数に立ち戻ってみると、
$T$ は実験開始からの時間
$X_t$ は処置前後を表す二値変数（0なら処置前、1なら処置後）
$T_i$ は処置が行われた時間 $T$ を表します。

でした。
介入を行わない場合、
$X_t$ はいついかなる時も0です。
また $T_i$ は定義できません。（無限大という考え方もできます。）
ということで、 $(T - T_i) X_t$ も介入前は全て0として扱っていましたから、これも0になります。

これを実装すると、

#反事実の作成
cf_data = data.copy(deep=True) 
cf_data['xt'] = 0
cf_data['xt(t-ti)'] = 0

とすれば良いです。ちなみにcfというのは反事実的な（counter-fuctual）の略です。

8.反事実を予測する

先ほどと同じように使用する変数を取り出し、1を挿入してから予測してみます。

#反事実を予測する
X_cf = cf_data[['t','xt','xt(t-ti)']]
X_cf.insert(0, 'cep', [1]*len(X_cf))
y_cf_predict = result.predict(X_cf)

9.反事実を描画する

plt.style.use('fivethirtyeight')

plt.figure(figsize=(16,8))
plt.title('ITS_test')
plt.xlabel('time',fontsize=18)
plt.ylabel('event', fontsize=18)
plt.plot(y, 'o')

plt.plot(y_cf_predict)

介入がなかった場合に時系列データがこのような推移をするという結果がよくわかると思います。
$Y = \beta_0 + \beta_1 T + \beta_2 X_t + \beta_3(T - T_i) X_t$ で後ろ2項が常に0の場合に相当し、
$Y = \beta_0 + \beta_1 T$ となります。 $\beta_1$ というのは前回記事で書いたように処置前の傾きの推定量ですから、
このような直線形になるわけです。

10.信頼区間を表示する

www.statsmodels.org

さて、今回の記事の肝はこれです。
Pythonの問題点は折れ線回帰（セグメント回帰）における信頼区間と予測区間の描出が難しいことにあります。

信頼区間と予測区間

結構信頼区間と予測区間は混同されがちではありますが、
信頼区間：実際の直線がこの範囲に入っている確率が1-α以上
予測区間：サンプルデータがこの範囲に入っている確率が1-α以上
というように信頼区間と予測区間は意味が違います。基本的には信頼区間の方が予測区間より狭いです。
今回欲しいのは信頼区間になりますが、予測区間についても一応実装を残しておきます。

さて、一般的に「回帰分析　信頼区間」などでググると出てくるのはwls_prediction_stdを用いた以下のようなコードではないでしょうか。

from statsmodels.sandbox.regression.predstd import wls_prediction_std
prstd, lower, upper  = wls_prediction_std(result)

これで、lower, upperを出力してみます。

出てくるのは予測区間です。これを混同した記事がかなりあるので注意してください。そして今回欲しいのは信頼区間です。これは今回のwls_prediction_stdでは出てきません。predictionなので。
tedboy.github.io
この公式ドキュメントを暇な時に読んでいただければ良いですが、これ以上の機能はないようです。困りましたね。

一般的なセグメント回帰、折れ線回帰に対して予測区間を表示するための実装としてはこのような実装がありますが、（ちなみに信頼区間もできます）

#信頼区間を抽出
from statsmodels.stats.outliers_influence import summary_table
st, data, ss2 = summary_table(result, alpha=0.05)

y_predict_l, y_predict_u = data[:, 4:6].T

plt.plot(y_predict_l, 'r--', lw=2)
plt.plot(y_predict_u, 'r--', lw=2)

#描画
plt.style.use('fivethirtyeight')

plt.figure(figsize=(16,8))
plt.title('ITS_test')
plt.plot(y_predict)
plt.plot(y_predict_cf[11:], 'r--')
plt.plot(y, 'o')


plt.xlabel('time',fontsize=18)
plt.ylabel('event', fontsize=18)

plt.plot(y_predict_l, 'g--', lw=2)
plt.plot(y_predict_u, 'g--', lw=2)

これではITSにおいて肝となる反事実のグラフにおける描画ができません。（とはいえ反事実はただの単回帰分析＋αなので実装はそこまで難しくないですが）

今回使うのは
www.statsmodels.org
これのsummary_frameを使います。ドキュメント見ても難しいと思うので実装していきます。

#事実データに対する信頼区間を返す
predict = result.get_prediction(X)
frame = predict.summary_frame(alpha=0.05)
y_predict_l = frame['mean_ci_lower']
y_predict_u = frame['mean_ci_upper']

#反事実データに対する信頼区間を返す
predict_cf = result.get_prediction(X_cf)
frame_cf = predict_cf.summary_frame(alpha=0.05)

y_predict_cf_l = frame_cf['mean_ci_lower']
y_predict_cf_u = frame_cf['mean_ci_upper']

frame というのはこのような表で、信頼区間、予測区間の上下を示してくれている表になります。mean_ci_lower/upper が信頼区間で、obs_ci_lower/upper が予測区間です。ちなみにobsというのはobservationの略で、新しくデータが「観測」されるとするならこの区間にきますよ、という予測区間の意味を反映しています。

この実装の良いところはほぼ同一の実装で事実、反事実ともに信頼区間を返してくれ、重実装にならないところです。
あとは信頼区間の間をいい感じに塗れば完成します。

塗るときはfill_betweenを使いましょう。

plt.style.use('fivethirtyeight')

#itv（intervention time）介入したところが何番目のデータか
#tiは上で定義済み（介入した時間）
itv = ti[0]
#tot(total time)総観測期間
tot = len(y)

plt.figure(figsize=(16,8))
plt.title('ITS_test')
plt.plot(y_predict)
plt.plot(y_cf_predict[(itv-1):], 'r--')
plt.plot(y, 'o')
plt.fill_between(np.arange(itv,tot),y_predict_cf_l[itv:], y_predict_cf_u[itv:], color='r', alpha=0.2)
plt.fill_between(np.arange(itv,tot),y_predict_l[itv:], y_predict_u[itv:], color='b', alpha=0.2)
plt.xlabel('time',fontsize=18)
plt.ylabel('event', fontsize=18)

これでいい感じのグラフができました。

おわりに

一般的にこういう統計的手法はRやSASなどを使いますが、Pythonでも可能です。
matplotlibやseabornがある分描画はかなりやりやすく、ライブラリの使い方が難しい程度で自由度はかなり高いです。
なんらかのものに引用する場合は一声かけるか引用を明示してくれるとありがたいです。なんらかの間違いはあると思うので。。

10000字書きました。疲れました。~~またいつか気が向いたらなにかを書きます。~~

→続編です。slope change（ $\beta_1 + \beta_3$ ）を求めて結果の解析を行う記事です。
syleir.hatenablog.com

おすすめの書籍

小児科診療 2021年 06 月号 [雑誌]

診断と治療社

Amazon

おそらく現状で唯一（他にあったらぜひ教えてください）分割時系列解析に触れた成書です。ぜひ。医学雑誌ですけど統計回で普通に統計の勉強になります。

syleir.hatenablog.com
上にも貼ってますが分割時系列解析の解説記事です。

syleir.hatenablog.com
統計的因果推論の初歩の初歩の解説記事です。

syleir.hatenablog.com
統計検定準1級レベルの時系列解析をまとめています。

余談

最近流行りのChatGPTに聞いてみたら大嘘吐かれました。

全実装

説明のための余計なコードを省略したものです。上からStep by stepで実行していただくとわかりやすいかもです。

#ライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

#ファイルをDataFrameとして読み込む
data = pd.read_csv("dummy_data.csv")

## 研究開始時点から経過した時間T
t = np.arange(0, (len(data)))
data["t"] = t

## 処置前後を表す二値変数Xt
x = np.where(data['date']>="2021-10-01", 1, 0)
data["xt"]=x

### 処置タイミングTiを取得、介入からの経過時間Xt(T-Ti)
ti = data[data['date'] == "2021-10-01"].index
data['xt(t-ti)'] = data['xt']*(data['t']-ti)

#変数の抽出
X = data[['t','xt','xt(t-ti)']]
y = data[['y']]

# 回帰モデル作成
mod = sm.OLS(y, sm.add_constant(X))
# 訓練
result = mod.fit() 
# 統計サマリを表示
print(result.summary())

#Xの0列目に'cep'というXと同じ長さの[1, 1, 1, ...]という列を挿入
X.insert(0, 'cep', [1]*len(X))
#学習したモデルから推測を行う
y_predict = result.predict(X)

#反事実の作成
cf_data = data.copy(deep=True) 
cf_data['xt'] = 0
cf_data['xt(t-ti)'] = 0

#反事実を予測する
X_cf = cf_data[['t','xt','xt(t-ti)']]
X_cf.insert(0, 'cep', [1]*len(X_cf))
y_cf_predict = result.predict(X_cf)

#事実データに対する信頼区間を返す
predict = result.get_prediction(X)
frame = predict.summary_frame(alpha=0.05)
y_predict_l = frame['mean_ci_lower']
y_predict_u = frame['mean_ci_upper']

#反事実データに対する信頼区間を返す
predict_cf = result.get_prediction(X_cf)
frame_cf = predict_cf.summary_frame(alpha=0.05)

y_predict_cf_l = frame_cf['mean_ci_lower']
y_predict_cf_u = frame_cf['mean_ci_upper']

###描画
plt.style.use('fivethirtyeight')

#itv（intervention time）介入したところが何番目のデータか
#tiは上で定義済み（介入した時間）
itv = ti[0]
#tot(total time)総観測期間
tot = len(y)

plt.figure(figsize=(16,8))
plt.title('ITS_test')
plt.plot(y_predict)
plt.plot(y_cf_predict[(itv-1):], 'r--')
plt.plot(y, 'o')
plt.fill_between(np.arange(itv,tot),y_predict_cf_l[itv:], y_predict_cf_u[itv:], color='r', alpha=0.2)
plt.fill_between(np.arange(itv,tot),y_predict_l[itv:], y_predict_u[itv:], color='b', alpha=0.2)
plt.xlabel('time',fontsize=18)
plt.ylabel('event', fontsize=18)

Syleir’s note

2020.4.1より統計検定やE資格の勉強の進捗を報告しています。統計検定準1級、E資格、G検定取得しました！当ブログへのリンクはご自由にどうぞ。