【統計的因果推論】分割時系列解析をPythonで結果の解析・解釈をする【ITS】

1. はじめに

前回の記事ではITSをPythonで実装しながら、視覚的にわかりやすいグラフを作るところまでを目的に実装してみました。今回の記事では視覚情報だけでなく、解析的にもわかりやすいデータを出力するコードを提供し、実務に耐えるような表を実装することを目標にしています。

記事①　分割時系列解析の基本
syleir.hatenablog.com
記事②　Pythonでの分割時系列解析の実装
syleir.hatenablog.com
過去記事2作です。適宜こちらの記事に立ち戻ります。前回記事を読んでからのご参加を推奨させていただきます。

2. 求めたいものを確認する

記事①より、変数の定義と分割時系列解析によって知りたいものを確認します。

　
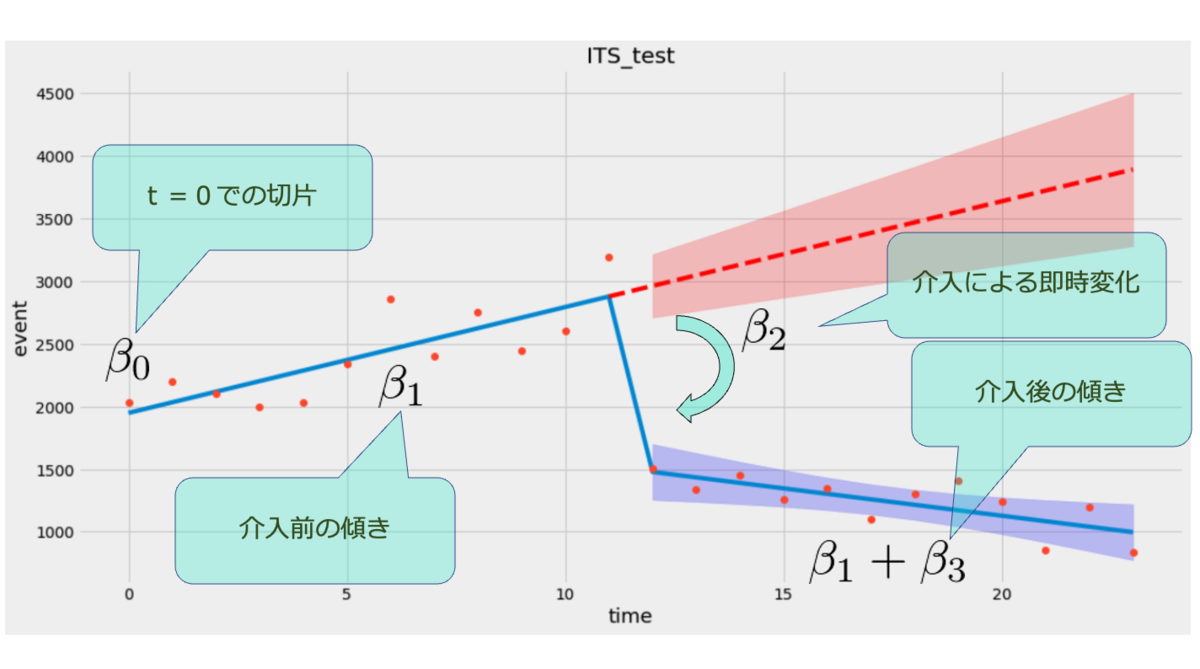
$\beta_0$ ：切片 intercept
$\beta_1$ ：介入前の傾き pre slope
$\beta_1 + \beta_3$ ：介入後の傾き post slope
$\beta_2$ ：介入前後の切片の差 level change
$\beta_3$ ：介入前後の傾きの差 slope change

でした。これが求めたいものになります。論文などでITSを使う際にはこれらのパラメータの点推定値、区間推定値、(p値)などが欲しいです。
前回記事②で実装した、サマリーによって出力が得られました。

これを見てみると、 $\beta_0 = 1948, \beta_1 = 84.41, \beta_2 = -1483, \beta_3 = -128.1$ ということを示唆すると捉えることができたのでした。
上述の5変数のうち、4つはこのモデルで求まりますが、 $\beta_1 + \beta_3$ はこれだけでは求まりません。
正確には $\beta_1 + \beta_3 = 84.41 + (-128.1) = -43.6$ と計算することで求まりますが、これらの変数は点推定値だけではなく、95％信頼区間も欲しいです。どれくらいの精度で推定できているのかも興味がある事項になります。
信頼区間については、サマリーでこの部分を確認すれば良いことになります。

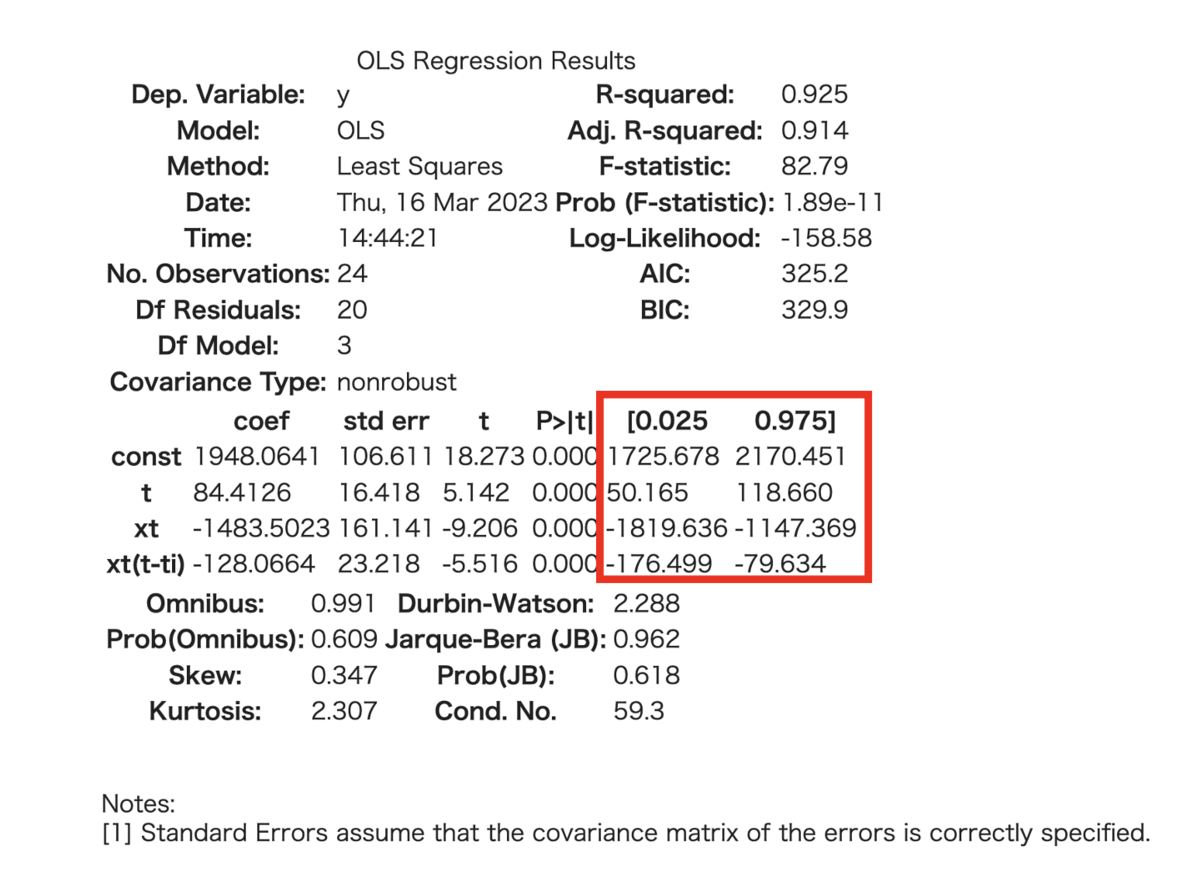
これにより、 $\beta_0 , \beta_1 , \beta_2 , \beta_3$ については点推定、区間推定ができているので、あとは $\beta_1 + \beta_3$ が区間推定できれば良いことになります。

3. $\beta_1 + \beta_3$ の推定の準備をする

これについては少しコツが必要です。
まずは、記事①で定義した式、

$Y = \beta_0 + \beta_1 T + \beta_2 X_t + \beta_3(T - T_i) X_t$ を変形します。
$= \beta_0 + \beta_1 T + \beta_2 X_t + \beta_3 T X_t - \beta_3 T_i X_t$ 　(展開する)
$= \beta_0 + \beta_1 T + \beta_1 T X_t - \beta_1 T X_t + \beta_2 X_t + \beta_3 T X_t - \beta_3 T_i X_t$
( $+ \beta_1 T X_t - \beta_1 T X_t$ を追加し、 $\beta_3$ の形に合わせる)
$= \beta_0 + \beta_1 T - \beta_1 T X_t + (\beta_1 + \beta_3) T X_t + \beta_2 X_t - \beta_3 T_i X_t$
( $+ \beta_1 + \beta_3$ の形を作る←この式変形の目的)
$= \beta_0 + \beta_1 T(1 - X_t) + (\beta_1 + \beta_3) T X_t + \beta_2 X_t - \beta_3 T_i X_t$
$= \beta_0 + \beta_1 T(1 - X_t) + (\beta_1 + \beta_3) T X_t + (\beta_2 - \beta_3 T_i)X_t$
(変数ごとにまとめる)
とします。
式変形しただけですが、介入後の傾き $\beta_1 + \beta_3$ が求まるモデルに様変わりしていることがわかります。
変数として採用するのが、 $T(1 - X_t), T X_t, X_t$ です。元々も3変数だったので自由度も変わらず、式変形しただけなのでこのモデルで予測される折れ線回帰も前回のモデルで実装したものと同じ結果が得られます。

4. 実装していく

前回の全実装部分を実行した後にデータの前処理を追加し $T(1 - X_t), T X_t, X_t$ の項を用意していきます。

data["t(1-xt)"] = data["t"] *(1 - data["xt"])
data["t*xt"] = data["t"] * data["xt"]

これで変数を追加しモデルを再構築します。

X = data[["t(1-xt)",'t*xt','xt']]
y = data[['y']]

# 回帰モデル作成
mod2 = sm.OLS(y, sm.add_constant(X))
# 訓練
result2 = mod2.fit() 
# 統計サマリを表示
print(result2.summary())

出力された結果が以下です。

式変形前のモデルと式変形後のモデルの学習結果を比較してみます。
（当然ですが、）偏回帰係数のパラメータ以外は全く同じものができています。

これらのパラメータを表にいい感じにまとめれば論文にも耐える形での実装が可能です。

5. おわりに

簡単ではありますが、PythonでのITSの実装例を提供しました。

小児科診療 2021年 06 月号 [雑誌]

診断と治療社

Amazon

この本で触れられている初歩的なものをさらに解説し、Pythonistaに向けた実装ができたと思います。この本では実際の論文を用いながら解説してくれているので併用しながら読んでみるとさらなる理解が深まると思います。

次は周期性のあるデータをITSで分析する記事を出そうかと考えています~~（いつになるかはわかりません）~~。
時系列記事のPart4あたりが予習に良いかと思います。ここまではただの折れ線回帰をお話していましたが、この辺から時系列ぽさが出てきます。
syleir.hatenablog.com

6. 全実装

前回実装と今回実装をまとめたものを出しておきます。

#ライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

#ファイルをDataFrameとして読み込む
data = pd.read_csv("dummy_data.csv")

## 研究開始時点から経過した時間T
t = np.arange(0, (len(data)))
data["t"] = t

## 処置前後を表す二値変数Xt
x = np.where(data['date']>="2021-10-01", 1, 0)
data["xt"]=x

### 処置タイミングTiを取得、介入からの経過時間Xt(T-Ti)
ti = data[data['date'] == "2021-10-01"].index
data['xt(t-ti)'] = data['xt']*(data['t']-ti)

#変数の抽出
X = data[['t','xt','xt(t-ti)']]
y = data[['y']]

# 回帰モデル作成
mod = sm.OLS(y, sm.add_constant(X))
# 訓練
result = mod.fit() 
# 統計サマリを表示
print(result.summary())

#Xの0列目に'cep'というXと同じ長さの[1, 1, 1, ...]という列を挿入
X.insert(0, 'cep', [1]*len(X))
#学習したモデルから推測を行う
y_predict = result.predict(X)

#反事実の作成
cf_data = data.copy(deep=True) 
cf_data['xt'] = 0
cf_data['xt(t-ti)'] = 0

#反事実を予測する
X_cf = cf_data[['t','xt','xt(t-ti)']]
X_cf.insert(0, 'cep', [1]*len(X_cf))
y_cf_predict = result.predict(X_cf)

#事実データに対する信頼区間を返す
predict = result.get_prediction(X)
frame = predict.summary_frame(alpha=0.05)
y_predict_l = frame['mean_ci_lower']
y_predict_u = frame['mean_ci_upper']

#反事実データに対する信頼区間を返す
predict_cf = result.get_prediction(X_cf)
frame_cf = predict_cf.summary_frame(alpha=0.05)

y_predict_cf_l = frame_cf['mean_ci_lower']
y_predict_cf_u = frame_cf['mean_ci_upper']

###描画
plt.style.use('fivethirtyeight')

#itv（intervention time）介入したところが何番目のデータか
#tiは上で定義済み（介入した時間）
itv = ti[0]
#tot(total time)総観測期間
tot = len(y)

plt.figure(figsize=(16,8))
plt.title('ITS_test')
plt.plot(y_predict)
plt.plot(y_cf_predict[(itv-1):], 'r--')
plt.plot(y, 'o')
plt.fill_between(np.arange(itv,tot),y_predict_cf_l[itv:], y_predict_cf_u[itv:], color='r', alpha=0.2)
plt.fill_between(np.arange(itv,tot),y_predict_l[itv:], y_predict_u[itv:], color='b', alpha=0.2)
plt.xlabel('time',fontsize=18)
plt.ylabel('event', fontsize=18)

###slope changeを求めるモデルを作る
#データの前処理
data["t(1-xt)"] = data["t"] *(1 - data["xt"])
data["t*xt"] = data["t"] * data["xt"] 

#変数を準備する
X = data[["t(1-xt)",'t*xt','xt']]
y = data[['y']]

# 回帰モデル作成
mod２ = sm.OLS(y, sm.add_constant(X))
# 訓練
result2 = mod2.fit() 
# 統計サマリを表示
print(result2.summary())